Methodological introduction
There is nothing to distinguish one part of space from another except its relation to the place of material bodies. We cannot describe the time of an event except by reference to some other event, or the place of a body except by reference to some other body. All our knowledge both of time and place is essentially relative.
J.C. Maxwell
One can philosophize endlessly about the integrity of the Universe, about the interconnection of all its elements, about man as a microcosm and many similar topics. At the same time, philosophy does not need a numerical measure, while science cannot do without it.
As soon as we ask ourselves a scientific question about the interconnection and integrity of the electron and the Galaxy, the human being and the star, the atom and the Universe, we will immediately have to determine the metrics of space in which we will search for this integrity. Immediately, we will face a certain obstacle. The point is that the scales of the microcosm and macrocosm differ by tens of orders of magnitude, and the scales of the macrocosm differ from those of the megamir by the same amount. How can we compare the life of a tiny electron and a giant Galaxy?
In everyday life, we deal most often with absolute comparisons. For example, we note that Ivan Ivanovich is 10 centimeters taller than Peter Petrovich, but his salary is 200 rubles lower.
However, once we go beyond single-type objects, we are forced to switch to a system of relative comparisons.
Take, for example, this statement: object A is larger than object B by 2.7 meters.
Does this statement tell us anything about the mutual difference of these objects if we don’t know what we are talking about? If we are comparing two trees, yes. If we compare two asteroids whose diameters are measured in kilometers, then the difference of 2.7 meters is lost in measurement errors. The same difference becomes absolutely insignificant and meaningless if it refers to two galaxies.
Meanwhile, this example was taken from Krylov’s fable about the elephant and the moss. The difference of 2.7 meters in this case is huge, because the three-meter height of the elephant is ten times greater than the thirty centimeter height of the moss.
This simple example shows that when we need to compare objects from the micro-, macro- and megaworld, we cannot do without a relative system of comparisons. The transition from absolute to relative system of comparisons can be likened to the transition from horizontal to vertical.
There is one more small detail that is not unreasonable to remind those readers who are not engaged in scientific work related to precise measurements. The fact is that if the size of an atom is 100,000 times smaller than the size of a living cell, and the cell is 100,000 times smaller than the size of a human being, this record still looks convenient. However, what about comparing the size of a proton to the size of the Galaxy? The proton is 100 000 000 000 000 000 000 000 000 000 000 000 times smaller.
Here, math offers a simplification. The above number can be written as \(10^{35}\) , where the degree of ten indicates the number of zeros.
To make life even simpler, mathematics switches from degree expressions to logarithmic expressions. Then the above-mentioned number \(10^{35}\) converted through the decimal logarithm to the number 35:
\[\log(10^{35})=35\]
Yes, instead of complex counting of zeros or ascending to a degree, we immediately move into the realm of two simple arithmetic operations: addition and subtraction. For example, if we want to know how many times smaller than a star a man is, we must subtract from the decimal logarithm of the average diameter of a star \(\log(10^{12})=12\) the decimal logarithm of the average size of a man \(\log(10^{2})=2\):
\[12-2=10\]
This means that a star is about \(10^{10}\) times larger than a human being. If you want to get a more “complete” impression of this comparison, you can write it down in expanded form: A STAR IS 10,000,000,000,000,000 TIMES LARGER THAN A HUMAN BEING.
In this paper, we will often use the logarithmic scale, because it greatly simplifies comparisons of micro-, macro- and megaworld parameters. Sometimes, keeping in mind the traditional forms of presentation, we will also use degree expressions. Sometimes we will decipher them for clarity.
So, for example,
\[10^2\ cm=1\ meter\]
\[10^{-3}\ cm=10\ microns\]
\[10^{-8}\ cm = 1\ angstrom\]
\[3\times10^{-18}\ cm = 1\ parsec\]
And one more methodological remark. The point is that the logarithmic scale, unlike the arithmetic scale, does not have quite the usual metric between unit divisions. Well, for example, if we want to show that object A is 3.16 times larger than object B, the size of which is equal to one meter, then on the arithmetic scale we will put off to the right a little more than three divisions, but on the logarithmic scale we will put off exactly five divisions. Thus, on the logarithmic scale, the transition from the dimensions of object B to the dimensions of object A will correspond to half of the distance from one to ten, which in the usual metric we associate with the number five. What is the point here?
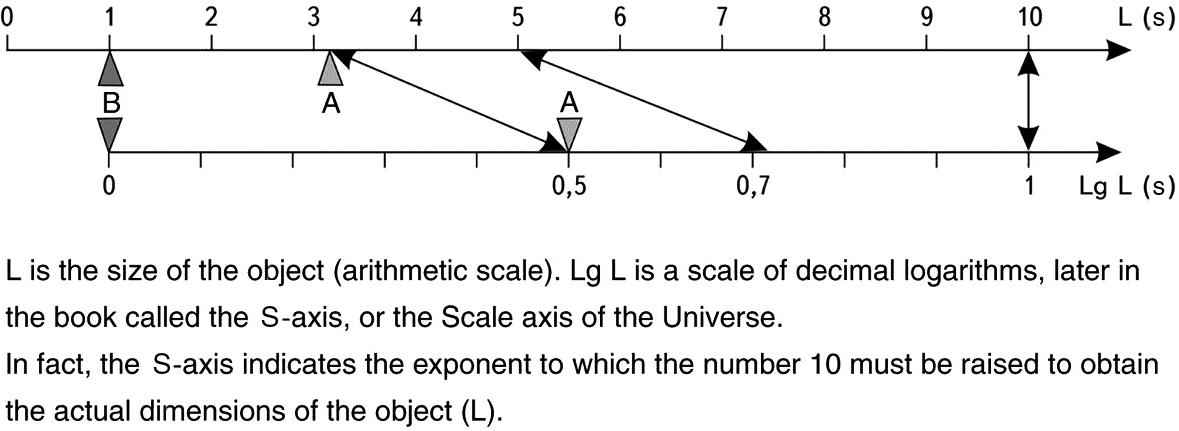
The point is that in the relative system of measures, the size of object A really lies exactly halfway between one meter and ten meters. In fact, if we multiply it again by 3.16, we get already object C, with dimensions of ten meters:
\[1\ meter\times3.16\times3.16 = 10\ meters\]
Therefore, the procedure of increasing by a factor of 3.16 is equivalent to a shift between divisions on the logarithmic (base 10) axis by 0.5 divisions.
It will be necessary to keep this feature in mind when we consider the fine structure of the scale order and translate objects close in size into logarithmic calculus. In this case, seemingly numerical discrepancies will often arise.
So, for example, a value of 31.6 microns would be converted to a logarithmic value as follows:
\[31.6 µm = 3.16\times10^{-3} cm = 10^{-2.5} cm\]
and the average human height is 1.6 meters:
\[1.6 m = 1.6\times10^2\ cm = 10^{2.2}\ cm\]
It should be remembered that all these and similar transformations do not change anything in essence, they are only different ways of expressing the same values. The values will be applied in one form or another solely out of convenience. In the process of reading this work, the reader is left to either believe that the author has repeatedly checked his calculations, or to remember this simple section of mathematics and check whatever he wants with a simple calculator that has a decimal logarithm function.
I would like to assure the reader, who will have to remember the seemingly so boring section of mathematics as the translation of ordinary numerical values into a logarithmic scale, that this translation makes it possible to compare very distant objects and their scales with each other. Thanks to this, the absolutely marvelous world of scale similarity of the Universe, in which we live, but which we pass by every day, opens before us. Therefore, it is safe to say that the reader’s labor to overcome mathematical difficulties will not be spent in vain.