S-factors (Coefficients of scale symmetry)

We have already mentioned that other parameters of our world should obey the laws of scale symmetry, besides dimensional relations: mass, number of elements, time, frequency, etc. However, the author had no possibility to make a similar analysis for all these parameters. But some proportions, which I stumbled upon while collecting information on dimensional ratios, have accumulated and are, I think, of some interest to the reader. We present them here for the completeness of the picture.

WE'LL START AT \(10^{10}\).

In ordinary reference books and encyclopedias, anyone can find the relations listed below, which, although they are approximate, are performed with an accuracy of one or two orders of magnitude:

"Scale bars" made of light beams.

• The Universe we see consists of \(10^{10}\) galaxies.
• The most common galaxies contain \(10^{10}\) stars on average.
• The SWman brain contains about \(10^{10}\) neurons.
• Each cell contains about \(10^{10}\) nucleotides in 46 chromosomes.
• In addition, fifty years from now, the Earth's population will be \(10^{10}\), and ecologists estimate that the SWman population should stabilize at this figure¹.

Those are the facts. Here's another very clear example.

We do not think much about the fact that the entire sea of light in the Universe consists not of continuous rays, but of short wave packets, because photons are emitted by atoms in quanta. TSWs, if a star shines in space, its rays are a "straw" of wave packets. In reference books on physics, you can find information that the time of emission of a quantum of light is \(10^{-8}\) seconds, and the speed of light is about \(10^{10}\) cm/s.

That is, the length of the wave packet is: Lc = \(10^{-8}\) s * \(10^{10}\) cm/s ≈ \(10^{2}\) cm.

So, if the average size of an atom is \(10^{-8}\) cm, then the length of a light "straw" equal to \(10^{2}\) cm is exactly \(10^{10}\) times the average size of an atom.

I.e., figuratively speaking, the WHOLE WORLD IS DESIGNED AS A "MASSIVE LINE" OF LIGHT RAYS WHOSE LENGTH IS \(10^{10}\) TIMES THE ATOMIC SIZE AND COMMENSURATE WITH THE AVERAGE HUMAN HEIGHT.

This fact lies on the surface, but in light of the large-scale patterns revealed in the book, it raises a lot of reflection.

THE SCALING FACTOR IS \(10^{20}\).

The analysis has shown that in the Universe the scale similarity with coefficient - \(10^{20}\) plays a great role. Any point on the S-axis (except for two extreme points) has at least two more structurally similar points.

For the macro-world, which is accessible to our direct influence, in any slice of the scale axis, we can find similar structures in the mega- and micro-worlds, which will be 20 orders of magnitude larger or smaller, respectively.

The coefficient \(10^{20}\) itself becomes a certain fixed scale of the Universe, a certain yard which many processes are considered. It can be found not only in structural similarity but also in many other proportions, both general (where it appears averagely) and particular (where it appears precisely).

HERE ARE SOME EXAMPLES OF THE \(10^{20}\) RATIO.

1. Normal STARS have an average size of - \(10^{12}\) cm and are made up of \(10^{-8}\) cm atoms.
2. WHITE CARLICLES - average size \(10^{10}\) cm, composed of highly compressed atoms of size \(10^{-10}\) cm.
3. NEUTRON stars, compressed by gravity very strongly, - up to \(10^{7}\) cm, consist of nucleons of \(10^{-13}\) cm in size.

IN ALL CASES THE SCALE "DISTANCE" BETWEEN THE SYSTEM AND ITS ELEMENTS IS THE SAME - \(10^{20}\).

Let us remind once again that stars are more than 90% of the matter of the Universe, hence S-COEFFICIENT \(10^{20}\) is the UNIVERSAL COSMIC PROPORTION.

4. PULSARs emit at a variety of frequencies. The full range of radiation is enormous. For example, "the ratio of frequencies at both ends of the SWge range of electromagnetic waves at which NP 0531 radiates is (\(10^{20}\):1) - a fantastically large value"².

The highest frequency of pulsar emission is the gamma-ray range, which exceeds 3 \(\times\) \(10^{27}\) hertz, the lowest frequency is the radio range, which is close to 3 \(\times\) \(10^{7}\) hertz (10 m wavelength), i.e. there is again a difference of 20 orders of magnitude between them.

5. In a new light, we can now consider the BIG NUMBERS PROBLEM. The values of the parameters used in obtaining the Big Numbers were chosen in such a way that they belong to the beginning of the Macro-interval and the end of the Mega-interval (see Fig. 1.4).

This resulted in doubled scale similarity coefficients close to (\(10^{20}\))\(^2\) = \(10^{40}\).

TSWs, the GENERAL STRUCTURAL INVARIANT has a length of 20 lengths on the S-axis and unfolds over the massive length of the Universe in three ways: in the MICROMIR, MACROMIR and MEGAMIR. At the same time, it is manifested not only in the similarity of the structures of these three worlds but also, as the above examples have shown, in the correlation of elements - system, in the relation of extreme frequency characteristics of stars, etc. We can be sure that in time a great number of other examples of manifestation of this coefficient of scale similarity will be found.

SCALE SYMMETRY COEFFICIENT (SSC) \(10^{60}\). We have already mentioned, according to M. A. Markov's model of the Micro-Macrosymmetric Universe, a maximon can be a Universe for its internal structure, and the Universe can be a maximon for the MetaUniverse, etc. (see Fig. 1.3). Based on this model, we can talk about the possible presence in Nature of global symmetry of similarity with the coefficient \(10^{60}\), and if such a similarity coefficient exists, then the regularities of changes in structures as they approach the edges of the scale interval (\(10^{-33}\) cm and \(10^{28}\) cm) will also be similar. Let us consider this question in more detail.

To begin with, the objects of the Universe on its many scale floors can belong to different types of structures.

For example, even a cursory glance is enough to detect the overwhelming dominance of spherical formations on scales from \(10^{9}\) to \(10^{13}\) cm (CLASS # 9) - stars. On the scale of \(10^{20}\)- \(10^{23}\) cm (CLASS # 11), galaxies have more varied shapes, among them there are not only elliptical and spiral galaxies but also flat and needle-shaped ones.

However, not only galactic floors differ from stellar floors by their average type of dimensionality. In the macrocosm, the atomic floors (CLASS # 5) of the Universe have predominantly nuclear-shell structures, while the cellular, organismal, and biocenotic floors (CLASS # 6-8) have polycentric and more complex structures. All this leads us to the assumption that each scale level of the Universe has its own inherent structure, the dominance of some particular types of forms and types of symmetry. Therefore, in this section, we will further analyze the global structural dimensionality of the Universe, a kind of macroview of global trends.

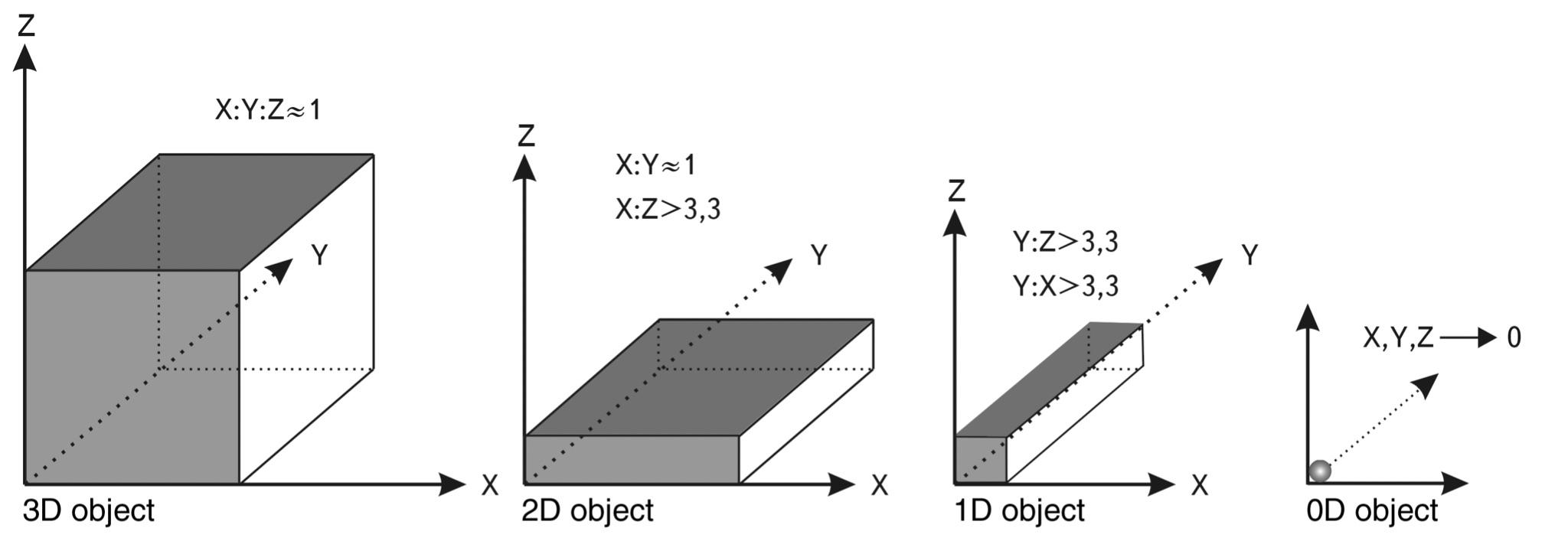
Fig. 1.45

METHODOLOGICAL DEPARTURE

In order not to go into the subtleties of structural analysis, let us limit ourselves to the most important criterion - the dimensionality of the system. We will distinguish the following main types of dimensions: zero-dimensional, one-dimensional, two-dimensional, three-dimensional and four-dimensional.

On the one hand, any real system in our world has at least three dimensions. Even a spider's web has a thickness in addition to its length. On the other hand, in all areas of natural science, we use the terms: linear, flat, volumetric... These terms already contain an idea of the dimensionality of the system.

Without special justifications (they will be given in the second book of the cycle), let us introduce a minimal criterion for "loss" of one of the dimensions: along it the system size should be smaller by a factor of 3.3 than along the maximum system size. The maximum coefficient of "loss" of one of the dimensions is approximately 1:10. Then any system can be easily divided by us into different dimensional types (see Fig. 1.45).

The only exception would be the four-dimensional type of system, where more complex separation criteria must be used, the introduction and justification of which we will also leave for the future.

So, let's start our review of global trends from the top, with METAGALACTICS.

Astronomy has accumulated a lot of irrefutable facts, which allowed by the end of the XX century to make the assumption that the Metagalaxy has a cellular structure. The average size of a cell is 100 megaparsecs (3 \(\times\) \(10^{26}\) cm). The entire Metagalaxy is almost 100 times larger than the average cell size, ~1.5 \(\times\) \(10^{28}\) cm.

What are the Metagalactic Cells?

At first, astronomers believed that they form something like foam or honeycombs. However, careful observations have shown that "galaxy clusters... form an essentially one-dimensional structure"³, hence, the "walls" of these "honeycombs" are actually "holes" (see Fig. 1.46). Therefore, it is more correct to compare the structure of the Metagalaxy with a volumetric wireframe consisting of elongated superscales⁴.

To be precise, the term "supercluster" is incorrect, because "numerical experiments show that the cellular structure has a primary origin and was formed before galaxies and galaxy clusters formed during the epoch of the gaseous phase of the Universe..."⁴. TSWs, only for cluster-scale formations (\(10^{25}\) cm) we can assume the natural crowding of galaxies together, although, taking into account the problem of "hidden mass", even here there is still much unclear. For example, it is still unclear whether the "wires" of the superclusters are connected in a single bulk structure (as depicted in Fig. 1.46) or whether each supercluster exists separately. In the latter case, we can compare the structure of the Metagalaxy to absorbent cotton, in which, however, each "thread" exists by itself and is not connected to neighboring "threads" in any way. Therefore, with some reservations, but we can accept the scale of \(10^{25}\) cm as some boundary separating the world of galaxies and their systems with the world of the internal structure of the Metagalaxy.

If this is true, then we can say that on mega-scales of \(10^{27}\)...\(10^{28}\) cm the world is dominated by one-dimensional structures, since the ratio of the length of these "superwires" to their diameter is 6:1 on average.

Fig. 1.46. "Up close" the cellular structure of the Metagalaxy may be as it is depicted in the drawing by Anya Abrikosova, a school friend of the author's daughter. This purely abstract fantasy "from nothing to do" could also be not accidental

Let us now go deeper, to scales of \(10^{25}\)- \(10^{26}\) cm. Here we enter the world of galaxy clusters and groups⁵. These are the ones that make up the filaments of super scatterings. The shape of clusters (~\(10^{25}\) cm) and groups (~\(10^{24}\) cm) is predominantly two-dimensional - they are mostly flat.

Astronomers often use the term "flat disk clusters" in this connection. Moreover, these clusters of irregular⁶ type are homogeneous in density and consist of the youngest galaxies (in particular, spiral galaxies). Therefore, if we talk about the present-day structure of the Metagalaxy, it is represented mainly by two-dimensional structures at scales of \(10^{23}\)- \(10^{26}\) cm.

Fig. 1.47. Dimensionality of space on the Planck length scales according to some physicists' ideas¹

However, there are also clusters of the "regular" type (the number of galaxies in them ranges from 200 to 11,000)⁷ , which mainly consist of old elliptical galaxies containing old stars of the first generation. They also differ from irregulars in that they are predominantly spherical in shape with a strong concentration of galaxies toward the center, where the density is sometimes 40,000 times higher than the average density of the distribution of galaxies in the Metagalaxy ⁸. If we take elliptical galaxies as a "cosmic" component of this world, and spiral galaxies as a living one, then clusters of the "correct" three-dimensional type inside the "neural network" of "living" elliptical galaxies can be perceived as some nodes of obliquity inside the "network of life".

So, if we talk about the STRUCTURE of our present Universe (and not consider the remnants of the structure of the Universe when it was very young and had an age of the size of the types of structures of the Universe:

4 → 3 → 2 → 1 → 0

This phenomenological generalization is difficult to explain from the position of classical astrophysics.

If we turn to the opposite, left edge of the scale range of the Universe, to the scale levels of the microworld, it turns out that something similar, although less reliably established, can be found there as well. We are talking about string theory, which pervades the submicrocosm. (see Fig. 1.47). Taking into account Markov's position regarding maximons as point null-dimensional objects, each of which may have the internal structure of the whole Universe, one can PROPOSE that ON THE MAIN "edges" of the Universe the only 1 billion years), then when passing from level to level, a reliable, but very mysterious, at first glance, tendency is manifested here. Level \(10^{21}\)- \(10^{23}\) cm. The morphological diversity of galaxies allows us to distinguish all dimensional types from zero-dimensional (quasars) to four-dimensional (spiral galaxies).

Level \(10^{23}\)- \(10^{25}\) cm. Galaxies are connected mainly in two-dimensional groups and flat clusters, i.e., the planar, two-dimensional structure dominates at the level of galaxy clusters.

Level \(10^{26}\) cm. The super slopes have predominantly one-dimensional structures. The linear, one-dimensional structure dominates.

Level \(10^{28}\) cm. If we take M. A. Markov's position, then the entire Metagalaxy is most likely a point, zero-dimensional object for an external observer.

A very simple and unexpected conclusion follows from all of this.

Starting from the level of the scale of galaxies and climbing higher on the scale ladder of the Universe, one finds a step-by-step decrease in dimensionality of the structure is symmetric. OF THE UNIVERSE THE DIMENSIONALITY OF THE STRUCTURE SYMMETRICALLY DECREASES.

Then, going from left to right along the S-axis, starting from maximons and reaching atoms, we will pass through the following sequence of increasing dimensionality of structures:

0 → 1 → 2 → 3 → 4

WHAT DO WE SEE IN THE CENTER OF THE S-axis? Without going into details, we can assert that in the material world studied by us to date, the highest diversity of forms, the highest complexity of structures and the highest diversity of dimensions are characteristic of the Biosphere, which in its scale range as a whole is very close to the SCALE CENTER of THE UNIVERSE (SCU) and far from its edges. And if we define the dimensionality by the criterion of the ratio of the number of connections per one node of the network, then in the neural network of the brain it becomes just fantastically multidimensional.

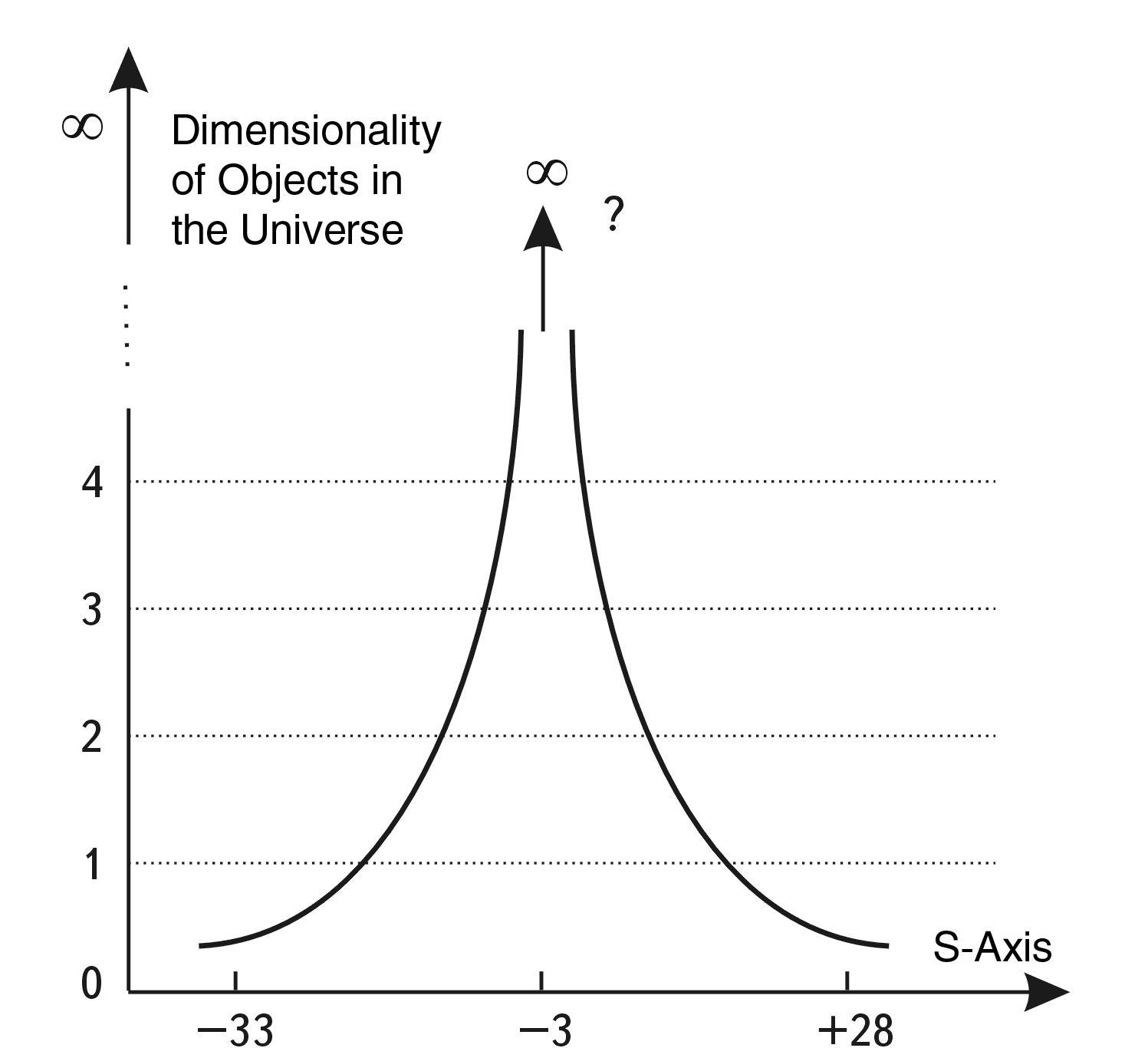Fig. 1.48. The dimensionality of objects in the Universe increases as we move away from its scaling edges (where the dimensionality tends to zero) and approach to the SCU

From all this we can draw a preliminary generalizing conclusion that the global complexity (and the dimensionality that is related to complexity) of the Universe increases from its scaling edges to its scaling center (Fig. 1.49).

Since structural complexity, as it will be shown in the third book of the cycle, is the foundation of information complexity of systems, if we trace with our mental gaze the path of complication of matter from the smallest particles of the microcosm and beyond, we will see a beautiful and mysterious phenomenological picture.

The complexity of objects and systems gradually increases from the microworld as one moves along the scale ladder, reaches a maximum in the central biological region of the S-axis, manifesting itself through the fantastic diversity of living forms, and then begins to gradually decrease until it reaches the main types of morphological diversity in the region of galaxies, and then rapidly decreases down to linear structures, ending with a zero-dimensional object, a "point" of the Universe, which, according to M. A. Markov's theory, becomes a freedmon for the Meta-Universe.

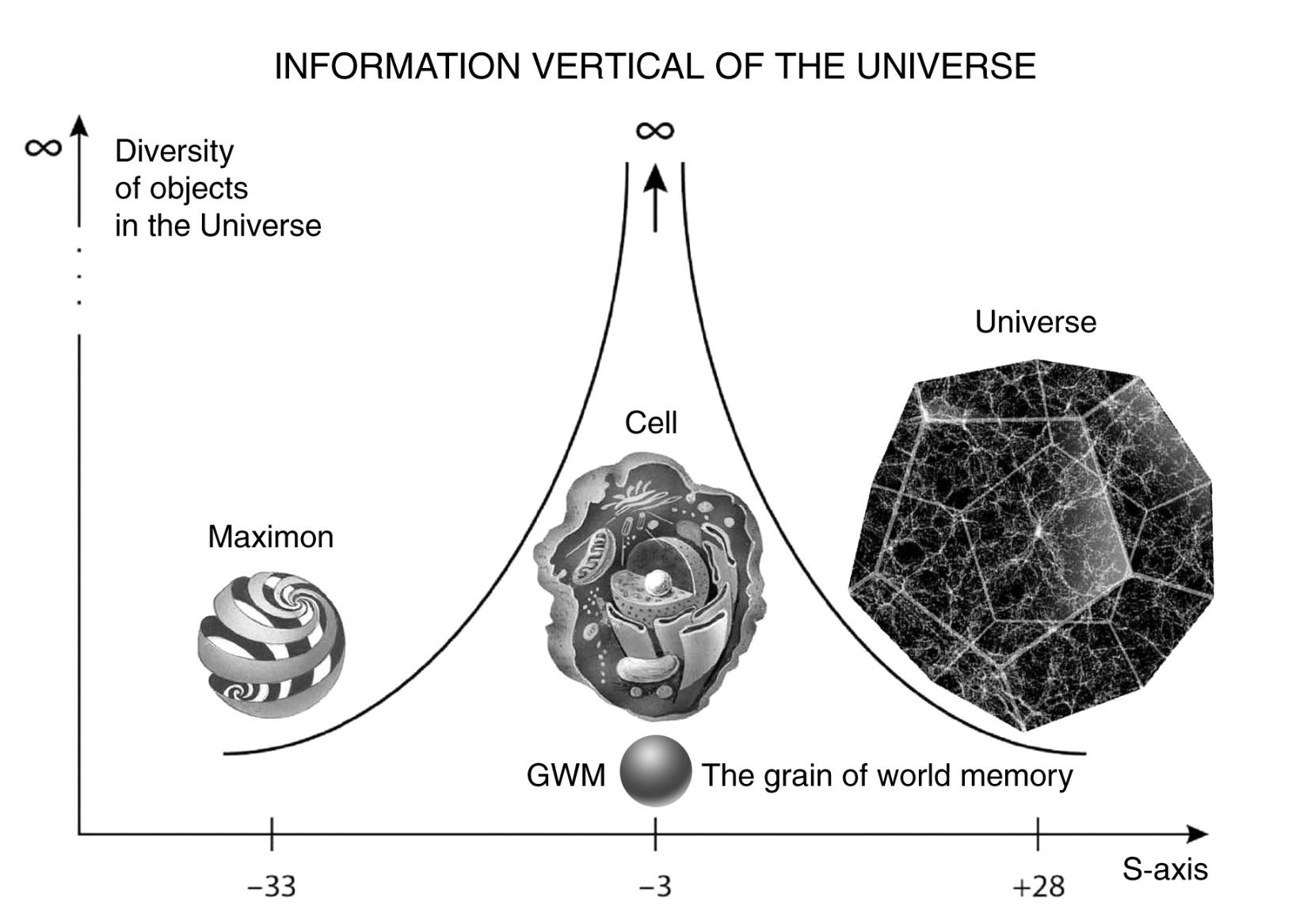Fig. 1.49. The diversity and complexity of objects grows as we approach from the edges of the scale range of the Universe to its center

This regularity is revealed only in the most general and approximate form and represents only an image, but in the following, we will show that this image hides the deep physical essence of large-scale interactions in the Universe.

Concluding this section, let us make an intermediate generalization and list the following RANGE OF COEFFICIENTS OF MASSAGE SUBJECT (SYMMETRY):

\(10^5\)- \(10^{10}\)- \(10^{20}\)- \(10^{60}\)

All of them are multiples of each other, and their combinations give rise to a number of intermediate dimensionless constants, for example: \(10^{15}\) - SCALE RANGE, \(10^{40}\) - LARGE NUMBERS.

So, after analyzing a large amount of material about the sizes of various objects of the Universe, we see that the phenomenon of Big Numbers, which occupied the minds of many physicists: Dirac, Gamow, Einstein, and others, is only a small part of the MASTER SYMMETRY of the Universe.

Closing on this section of the general STATIC description of the MASTER SYMMETRY of the Universe, we should add that the author has now accumulated much more factual material, which would confirm the existence of scale symmetry than is given in this part of the work. Basically, this additional material allows us to specify or add some particular aspects of the presented model, but from it it is possible to obtain, besides, information about subtle features of scale symmetry.

In the next chapter, we take only the first step in this direction.

1. Fundamentals of Ecology. SPb.: Special Literature, 1998. С. 158 ↩ ↩2

2. Shklovsky I. S. Stars. Their birth, life and death. Moscow: Nauka, 1977. С. 309. ↩

3. Large-scale structure of the Universe. / Edited by M. Longyear and J. Einasto. M.: Mir, 1981. С. 278. ↩

4. Large-scale structure of the Universe. / Edited by M. Longyear and J. Einasto. M.: Mir, 1981. С. 277. ↩ ↩2

5. Vorontsov-Vel'yaminov B. A. Extragalactic Astronomy. M.: Nauka, 1978. С. 407. ↩

6. Vorontsov-Vel'yaminov B. A. Extragalactic Astronomy. M.: Nauka, 1978. С. 271-272. ↩

7. Aghekyan T. A. Stars, Galaxies, Metagalaxy. M.: Nauka, 1981. С. 216. ↩

8. Aghekyan T. A. Stars, Galaxies, Metagalaxy. M.: Nauka, 1981. С. 213, 215. ↩