Standing S-waves of the Universe
Returning to the obtained results, we must recognize that the location on the S-axis of the most representative objects of nature often has such a high accuracy that one suspects that this accuracy is absolute. From our point of view, one of the mechanisms that could give rise to this accuracy of the S-interval partitioning of the Universe is harmonic oscillations in four-dimensional space that give rise to knots - three-dimensional stable systems. Let us consider this preliminary HYPOTHESIS in more detail. As it is known, STANDING WAVES are formed in such a way that their length is always an integer number of times within the total length of the excited medium. In this case, we are talking about the scale length, and we take the scale axis as the fourth spatial dimension, as we have already mentioned. However, the multidimensional mechanism of the model is very difficult to understand without first involving analogies from the one-, two-, and three-dimensional worlds familiar to us. Therefore, let us begin with the simplest, one-dimensional example.
Take a string clamped on both sides and create excitation on it (Fig. 2.39). The string is a linear system, the excitation occurs in a plane, and the standing wave node is a point object. Let us abstract from the real thickness of physical systems and consider their dimensionality further in accordance with the dominant extension.
In this case, it can be written that:
\[N_y = N_c - 1 = 1 - 1 = 0\]
\[N_d = N_c + 1 = 1 + 1 = 2\]
where \(N_c\) is the dimensionality of the system, \(N_y\) is the dimensionality of the standing wave node and \(N_d\) is the dimensionality of the motion space.
So:
\[N_y = N_c - 1, N_d = N_c + 1 \tag{2.1}\]
Suppose now that this condition is satisfied for any values of \(N_c\).
From the one-dimensional medium of the string, let us pass to a two-dimensional (\(N_c = 2\)) medium, for example, a round flat membrane - a drum membrane (Fig. 2.40). Pouring sand on it and hitting it in the center, we will find that after some time all the sand has gathered into linear ring structures (\(N_y = 1\)), which as if mark those places on the membrane where no motion occurs, i.e. represent to us linear "nodes" of standing waves on the plane.
Thus, it is easy to see that the relation (2.1) holds for \(N_c = 2\), since the standing wave nodes on the plane are circular linear formations, and the excitation propagates perpendicular to the plane - in a three-dimensional medium.
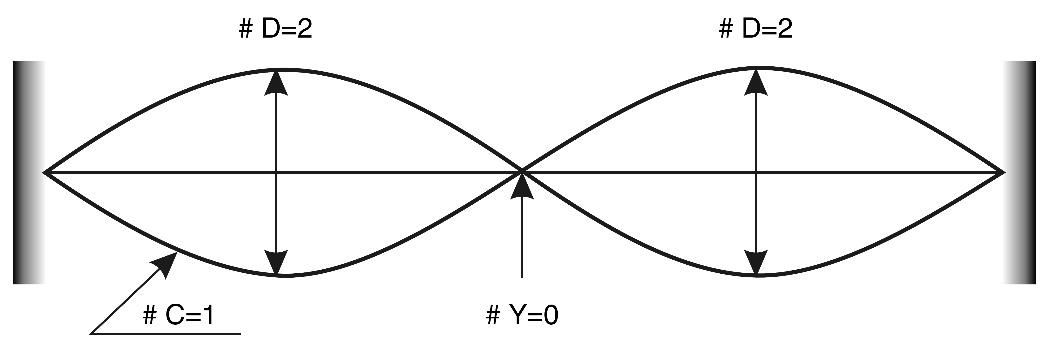
Fig. 2.39. Oscillations of a stretched string (1st overtone). \(N_d = 2\), \(N_c = 1\), \(N_u = 0\)
Let us pass from a two-dimensional medium to a three-dimensional medium (\(N_c = 3\)). Following only formal logic, we will have the dimensionality of nodes equal to two (flat partitions of volume cells), but the excitation will take place in a four-dimensional medium (\(N_d = 3 + 1 = 4\)). What is four-dimensional excitation?
The author's earlier work1 analyzed the well-known idea that the fourth spatial dimension is orthogonal to three-dimensional space.
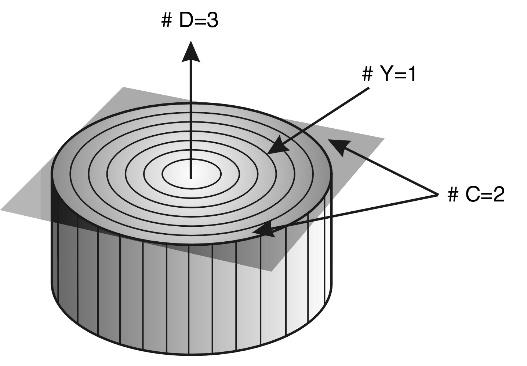
Fig. 2.40. Poured sand forms rings when the drum membrane oscillates
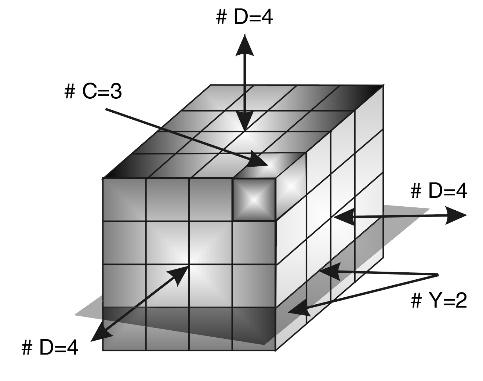
Fig. 2.41. Cells with fixed partitions appear inside the cube during oscillations
In a special case, we can consider that the forced pulsations of the three-dimensional volume (Fig. 2.41), its periodic contraction-expansion should lead to three-dimensional standing waves, whose nodes are cell partitions. With these reservations, we can assume that condition (2.1) remains valid for a medium dimension equal to three.
FREE REASONING
We will omit a rather long system of proofs that the scale dimension may well claim to be the fourth geometric space. This will be done in the next book by the author2.
The topic of additional dimensions of our space has been discussed in the literature since the last century, although it has an even older history. In particular, in the review paper by Y. S. Vladimirov3 it is shown that modern physics does not leave attempts to identify which parameter can claim to be the fourth dimension (in Y. S. Vladimirov's book it is called the fifth dimension).
From our point of view, the world is multidimensional, but human civilization comprehends this multidimensionality step by step4 reflecting the surrounding world in models, the dimensionality of which space is always equal to N + 1, where N is the current dimensionality of the world models of this or that civilization, and 1 is an additional dimension - time.
At present, since the Renaissance, the 3+1 model has been established in scientific thinking, but we are sure that time is not a single parameter of our world, but a set of not cognized, not yet revealed dimensions, so it would be more correct to write that at present the scientific paradigm is based on the model of the world with dimensionality 3+X, where X is the multiplicity of dimensions perceived by us as time. The author's research has shown5 that after 2000, mankind should make the next step in comprehension of the multidimensionality of our world, and then after some time, we will get the model of the world with dimensionality 4+X. In the transition period, the model should be 3+1+X, where the additional dimension to the three already revealed ones is an S-dimension. Let's see whether the formally constructed model (see Fig. 2.41) has any experimental confirmation? Let us set up a mental experiment in which a cubic volume of liquid saturated with light particles (suspended matter) is subjected to compression. Are volume cells with two-dimensional partitions formed inside such a liquid?
To verify this assumption, thank God, there is no need for special research. All the experiments we need have already been set up long ago and many times. For example, a cooling liquid metal alloy is the very model we described above. After all, if there are various impurities in the liquid medium of the base metal, then as it cools, the volume of the casting will be compressed on all sides, providing the compression we need orthogonal to three-dimensional space. And what is it? Yes, what is well known to all metal scientists - any alloy in the process of solidification is filled with so-called grains, two-dimensional boundaries between which are formed by suspended matter (additives, pores, etc.). These boundaries are two-dimensional nodes of four-dimensional oscillations of a three-dimensional medium (see condition (2.1) on pg. 356).
Following further formal logic, let us increase the dimensionality of the medium by one more unit (\(N_c = 4\)). If in such a four-dimensional medium a motion orthogonal to it is created (\(N_d = N_c + 1 = 4+1=5\)), then nodes will be formed in it, whose dimensionality will be equal to three (\(N_y = N_c - 1 = 4 - 1 = 3\)). What are these nodes? Formally speaking, they are three-dimensional bodies whose stability is conditioned only by the fact that they are nodes of five-dimensional oscillations in a four-dimensional medium. It is not difficult to guess that three-dimensional knots are our stable world of objects of the Universe! Protons, atoms, cells, planets, stars, and even man himself are all complex superpositions of vibrations of four-dimensional space.
The duration of existence of all systems of the Universe, and stability to external influences, therefore, is connected with the power of a node, i.e. with the energy of oscillations generating it. The description of the whole variety of life in the Universe can be realized with the help of the theory of waves and oscillations, but in a medium of higher dimensionality than the traditional physics has used so far. So, we have put forward a very important HYPOTHESIS. The whole world of stable objects of the Universe surrounding us are nodes of standing waves of complex harmonic oscillation in a four-dimensional medium.
The construction of a wave picture of the Universe with a high degree of theoretical accuracy is a matter of the future since this task is grandiose. Here we will take the very first steps along this path. For this purpose, let us simplify the conditions by reducing the whole consideration to the projection of four-dimensional space on a one-dimensional axis. This projection is precisely the S-axis, each point of which is a three-dimensional world of the chosen scale. For example, point (-8) is the universe of atoms, point (+12) is the world of stars, etc. F The projection of the five-dimensional motion in this model will be perpendicular to the S-axis, hence it will occur in the plane of the figure. Nodes of standing waves are points on the S-axis, which are coordinates of particularly stable dimensions of three-dimensional objects of the Universe.
We have already mentioned that in the Universe all matter is mainly concentrated in atoms (their nuclei) and stars (their nuclei). Consequently, it is well-known which zones of the scale hierarchy of the Universe are populated by the most abundant and long-lived systems. Let us see whether these zones of increased stability on the S-axis, which we described in Chapter 2.1, correspond to the points that can be obtained using the model of standing five-dimensional waves in a four-dimensional medium.
Let us consider the entire S-interval of the Universe, rounding all values of its left and right edges to integers and assuming the size of the Metagalaxy to be \(10^{27}\) cm, which corresponds to its age of 1 billion years. These temporal assumptions will allow us to show more convexly the fundamental aspects of a simplified version of the model. The first main tone, which is excited from five-dimensional space (Fig. 2.42), sets the edge points of the S-interval: the left node (-33) is the maximon and the right node (+27) is the Metagalaxy.
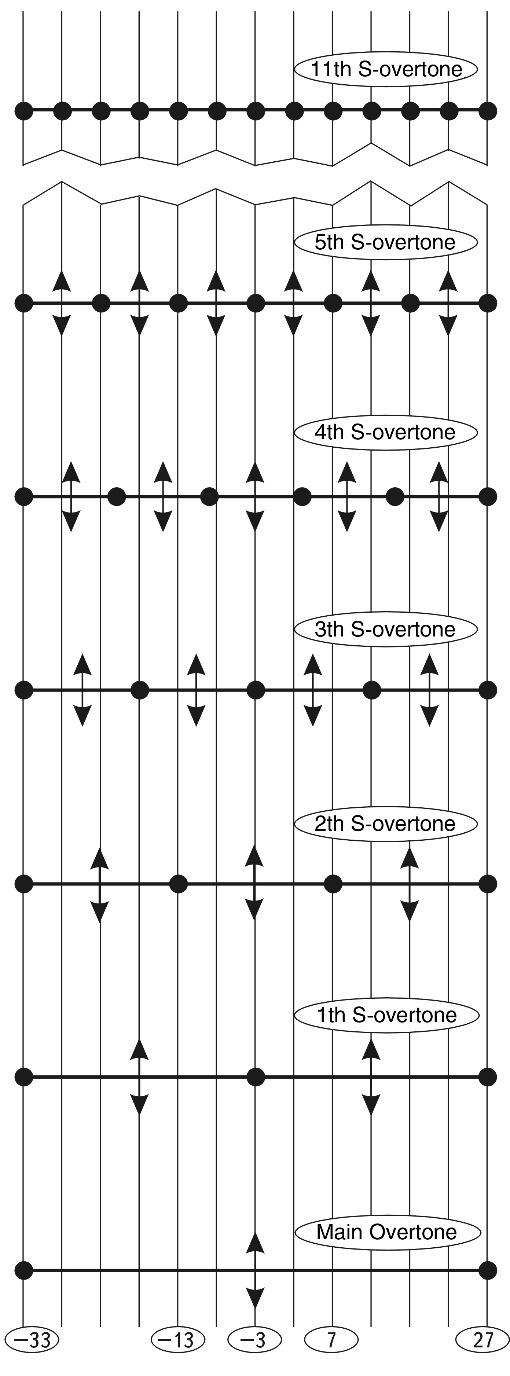
Fig. 2.42. Harmonic oscillations on the S-axis (simplified model)
The main tone beam has a coordinate (-3), which corresponds to 10 microns. In accordance with the accepted logic, the maximon and the Metagalaxy itself are the nodes of the STABLE WAVE OF THE MAIN TONE, so they are the most stable systems of the Universe, possessing the ultimate for it stability to external perturbations and the maximum duration of life. We can say that as long as the Universe exists, maximon exists in it. And vice versa, the maximon environment sets us as the initial substrate of the Universe.
The center of the scale interval is a size of about 10 μm at which the oscillations of the four-dimensional medium reach their maximum. Accordingly, it is dynamically the most pronounced scale in the Universe for a given rank of oscillations.
What physical interpretation can be given to the obtained slice of the Universe - the Universe of the basic tone?
Very simple - it is a physical vacuum (or ether), in which there is not a single material object and which is filled with vibrations, the maximum density of their energy is reached in the range of wavelengths from 10 to 100 microns (recall that in the refined model the scale center is shifted to the right and by virtue of the bimodality of SW occupies some range).
In fact (see Fig. 2.42), according to the accepted logic, only Nodules have a stable state in this environment. There are only two of them: MAXIMONS (-33) and METAGALACTICS (+27).
So that atoms, stars, etc. can appear in this medium, it requires the appearance of knots inside the S-Interval, on the sizes of atoms, stars, etc. But they do not yet exist in the main tone of the Universe.
Thus our model ether does not simply consist of maximon, they pulsate (oscillate along the S-axis) and generate in their medium the whole spectrum of wavelengths from \(10^{-33}\) cm to \(10^{27}\) cm (excluding extreme values), i.e. it is filled with its own energy, which is generated not by stars or matter, but by the medium of maximon (in traditional physics - field).
What phenomenon in the Universe could correspond to these oscillations? Obviously, the so-called RELICT radiation, but is it a relic in this case? Here we again return to the idea that the process of formation of matter from vacuum did not end in the first moments after the Big Bang, and the interaction of matter with the physical vacuum is still going on.
Does the conclusion about the constant activity of the ether due to the excited main tone of large-scale oscillations give us any prediction possibilities? Yes, the maximum activity of this radiation should fall, according to the refined model, on a wavelength close to 50 microns. What is the real picture? According to the accepted cosmological model, the spectrum of relic radiation should correspond to the spectrum of blackbody radiation, which is described by the Planck curve. The maximum in this case falls at 1.5 mm or \(10^{-0.9}\) cm. In our refined model, the maximum (the main tone beam) falls at a wavelength in the neighborhood of 50 μm, or \(10^{-2.3}\) cm. Thus, the model maximum is 1.4 orders of magnitude to the left of the conventional maximum. For a first approximation model, getting an error of one and a half orders of magnitude at 60 orders of magnitude is not a bad result. Thus, we have considered the basic M-ton with its nodes and bundles. In further consideration, we will simplify the problem and consider only the nodes of standing M-waves. Let us return to the simplified model.
The first overtone sets us a node (-3) in the SCU in the scale center of the Universe, which has a size of about 10 µm (see Fig. 2.42). We can assume that the first M-overtone of the Universe creates some massless superstable mysterious systems in a vacuum, which are completely unknown to science. If maximons are deduced at least theoretically, these unknown grains without flesh, grains of "spirit of world space" were not deduced earlier even theoretically, let alone to find them experimentally. Further, we will come back to these new "objects".
The second overtone gives us two additional stability points on the S-axis: (-13) and (+7). Let us see what this slice of the Universe represents. The left point is the size of nucleons, the right point is the size of neutron stars (or in a more general sense, the nuclei of stars).
So, at the second overtone, we have obtained the main basic material composition of the Universe: these are the nuclei of stars consisting of nucleons.
The fact that such systems are the final stage of development of many kinds of stars is a well-known fact. The fact that the matter of the Universe is more than 99% concentrated in these systems is now also a well-known fact. But we note additionally that the lifetime of nucleons (\(10^{56}\) years) and the nuclei of stars is the longest among all known material systems of the Universe.
In addition, the second overtone also sets us with fantastic accuracy the above-discussed division of the S-interval into three sections of dominant types of interactions.
Consequently, it can be stated that the whole variety of interaction types is conditioned by the influence of the second M-overtone on the primary four-dimensional medium of the Universe.
The third overtone gives us two more new points: (-18) and (+12). The left point, according to our assumptions, is the size of the electron. The right one, as already noted, is the average size of stars.
The fourth overtone sets four new points on the S-axis: (-21), (-9), (+3), (+15). The author has no physical interpretation of these nodes, so we leave them without comments.
The fifth overtone has a dedicated position in this hierarchy because it sets points on the S-axis that correspond exactly to the points of the main tone and the first two major overtones. Thus, its sustained M-zones include the sustained M-zones of the first three harmonics. To them, the fifth overtone adds only two stable points of its own on the S-axis: (-23) and (+17).
We see now that half of the series of stable objects of the Universe, which we obtained as a result of the previous empirical generalization, is determined by the fifth S-Overtone of the Universe (see Fig. 2.42), since all nuclear objects exactly correspond to the nodes of this overtone, forming the nuclear stability series:
-33 - Maximons;
-23 - electron nuclei (?);
-13 - atomic nuclei, proton;
-3 - cell nucleus;
+7 - the cores of stars;
+17 - galactic nuclei;
+27+1 - Metagalactic.
In this series, the most stable objects of the Universe alternate in 10 orders of magnitude. If the intervals between them are divided strictly in half, a structural series is formed, shifted relative to the nuclear one by 5 orders to the right, the objects of which also alternate in 10 orders, the so-called structural series of stability:
-28 - photons (?);
-18 - electrons (?);
-8 - atoms;
+2 - human;
+12 - stars;
+22 - galaxies.
Note that the objects of the structural series appeared on those places of the S-axis, which in the fifth M-overtone correspond to its bunches. The bundles, according to the logic adopted here, are zones of increased energy but decreased stability.
For stars and atoms, such a contradiction is alarming. A way out can be found if we consider the 11th S-Overtone (see Fig. 2.42), in which half of the nodes correspond exactly to the nodes of the 5th S-Overtone, and the other half of the intermediate nodes are defined mainly by the 11th M-overtone.
Hence the CONCLUSION that exactly 12 harmonics (the main tone and 11 overtones) are sufficient to obtain a model that gives an exact correspondence to the phenomenologically constructed series of the main objects of the Universe (see Fig. 1.7). However, the question arises, what about the nodes of the 4th, 6th, 7th, 8th, 9th and 10th overtones?
To answer this question, it is enough to plot the total stability curve of the 12 first S-harmonics (see Fig. 2.43). We see that it clearly shows some periodicity through 5 orders of magnitude, which indicates that the nodes of these 12 harmonics are mainly concentrated around 13 points on the S-axis. THESE ARE THE POINTS WHERE THE SIZES OF THE MAIN CLASSES OF SYSTEMS OF THE UNIVERSE ARE LOCATED.
The other harmonics give only a secondary fractal ripple on the stability curve. Hence it follows CONCLUSION that, since for the majority of S-Harmonics the nodes appear in the same row, which is a multiple of 5 orders, a MASTER-HARMONIC RESONANCE is realized in Nature.
Thus, we see that our model gives a sufficiently complete correspondence of the nodes of scale harmonics to the position on the S-axis of the main classes of systems of the Universe. It is simply unrealistic to wish for more correspondence at the first stage of building the theory of scale-harmonic oscillations.
WHAT DOES THAT MEAN?
Firstly, the Universe has as it were many S-frequency slices (layers), each of which defines its own HIERARCHICAL RANGE OF SUSTAINABLE SYSTEMS. The first slice is the etheric Universe, the second slice is the informational Universe, and the third slice is the material Universe of basic systems. The twelfth slice (the 11th overtone) sets us the structure of the Universe in its usual material incarnation: photons, electrons, atoms... stars, galaxies, and their nuclei. Although the twelfth slice already has stability points for such systems as cells and animals, it still needs intermediate stability zones where macromolecules, pre-cellular structures, and other subsystems of complex hierarchical systems could be formed.
As the author's earlier study6 has shown, protein living systems are distinguished by the fact that their scale-hierarchical organization is extremely densely packed. For the scale axis, this is achieved when each system of a higher hierarchical level is on average 3.16 times larger than the size of its elements. On the S-axis, points with such a step form a periodicity with an interval of 0.5 orders of magnitude.
Since the universal S-interval contains 60 orders (in the simplified model), its corresponding partitioning can be given only by the 120th harmonic. From this, it is possible to conclude that the possibility of the existence of protein life is supported by the S-overtone not lower than the 120th order. However, in this case, the S-structure of life should penetrate all scale levels, including the microcosm and cosmos.
An alternative variant of the empirically revealed S-periodicity with a step of 0.5 orders is the mechanism of localization of S-harmonics. For example, if we "cut out" from the S-interval of the Universe 15 orders, which are occupied by protein life (from viruses to biosphere), then within this scale range of protein life the S-axis partitioning with a step of 0.5 orders is obtained already at the 30th harmonic (15 : 0.5 = 30).
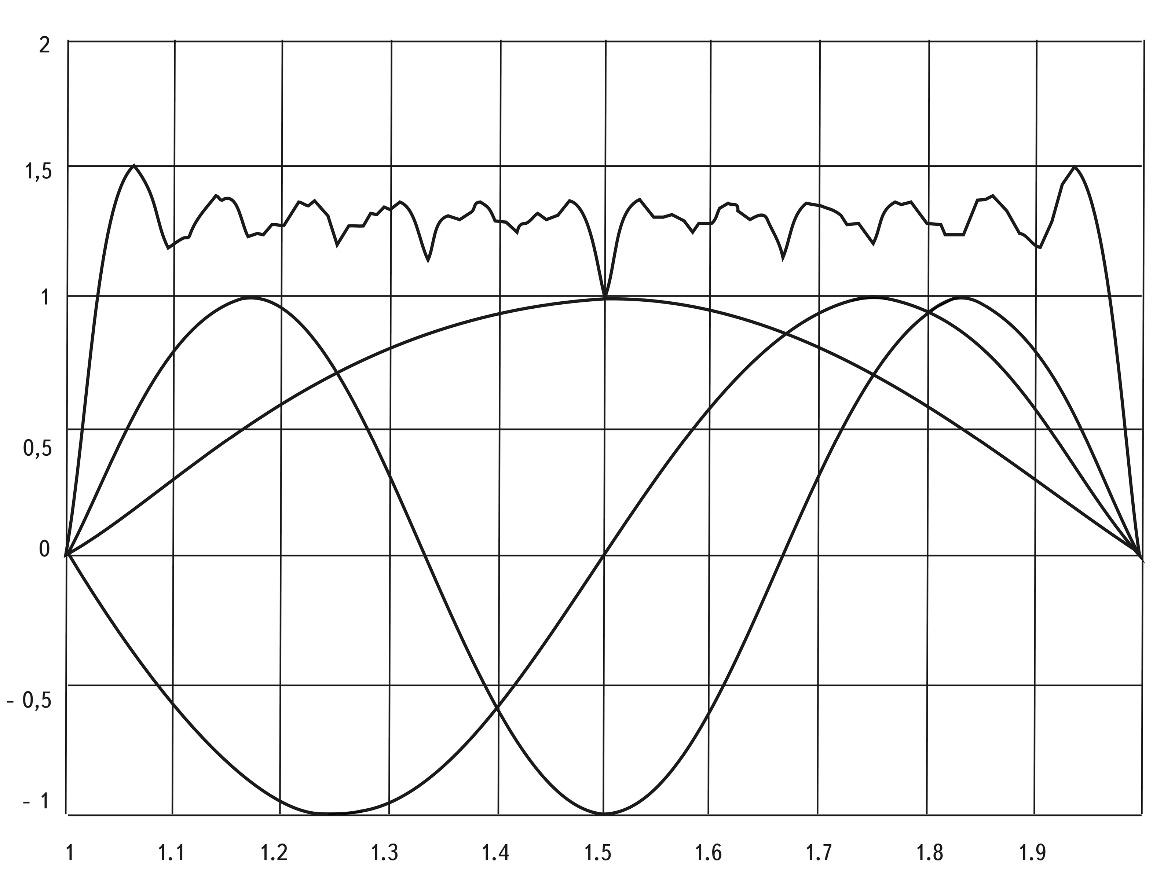
Fig. 2.43. Graph of the sum of standing waves of the first 12 harmonics (simplified model)
For convenience in plotting the graph, let us take the interval from 1 to 2. Then we can write that \(X \in [1; 2]\), where X is simply a number.
\(\lg L \in [-33;+27]\) is the S-interval.
\(\lg L = -33 + 60 (X - 1)\) is a scale for converting X to L.
Then the point X = 1 on the graph corresponds to \(\lg L = -33\), i.e. the size of the maximon. The point X = 2 corresponds to \(\lg L = +27\), i.e., the size of the Metagalaxy, and the point X = 1.5 corresponds to \(\lg L = -3\), i.e., the point of the SCU, etc.
To consider our theoretical model of the stability of the objects of the Universe, we plot the graphs of musical harmonics, where n is the ordinal number of the harmonic. \(y = \sin (n \pi X)\) is the graph of the function of the harmonic with the ordinal number n.
$$ Y = \frac{2}{N} \sum_{}^N \left| \sin (n \pi X) \right| \tag{2.2} $$
the sum of the functions of N harmonics, where 2/N is a coefficient equalizing the energy of all harmonics to a total of 1.
Below are the graphs of the first three harmonics, while the upper curve represents the result of summing the modulus of the amplitudes of standing waves for the first 12 harmonics (N=12) according to equation (2.2).
This curve provides insight into the potential stability/instability of objects, or, in other words, it represents the function of the energetic instability of objects as a function of the logarithm (\(\lg L\)) of their sizes.
The lower the value of Y, the more stable the object corresponding to X (where the size of the object is calculated using the formula: \(\lg L = -33 + 60(X - 1)\)).
It can be observed that the most stable objects, excluding maximons and the Metagalaxy itself, are those whose sizes fall within the MCV.
If we convert the X-values of all "troughs" (1<Y<1.5) into logarithmic size values, it turns out that the entire sequence of known cosmic objects falls into these "troughs".
The author expresses gratitude to A. G. Ivanov for assistance in the mathematical formalization of the idea.
In any case, we see that to explain all regularities of the hierarchical structure of protein bodies it is necessary to complicate the model of S-harmonics to much higher overtone levels. Therefore, we will leave this problem for further work. Second, since the number of S-Overtones can be potentially infinite, no point on the S-axis has zero stability. Another issue is that the power of each subsequent overtone decreases, hence the degree of stability due to its nodes also decreases. Therefore, the picture of the general stability of the objects of the Universe depending on their sizes will most likely have a FRACTAL VIEW.
Hence - DUALISM OF STRUCTURE OF SPACE. On the one hand, it is quantized, and quantization should be especially pronounced near the main nodes of the S-axis, and on the other hand, it is continuous since the higher overtones create a continuous series of stability.
Some parts of the S-axis will be predominantly quantized (around the main knots), and others - predominantly continuum (scale levels maximally removed from the main knots).
This explains, from our point of view, the fact that microphysics is successfully described by quantum theory, and macrophysics does not need it.
One can only PROPOSE that also for the physics of stellar nuclei (because of the power of the node of the 2nd overtone - (+7)) quantum effects are essential, which at present are simply not detected yet.
In general, it is not difficult to obtain a mathematical expression for the integral stability of the objects of the Universe based on the addition of the harmonics of the Fourier series (see Fig. 2.43). Undoubtedly, the obtained dependence is of a qualitative and principled nature; in the future, it requires further clarification and concretization.
Let us return to the PROPOSITION that the Universe consists of four-dimensional layers nested into each other, each of which has its own frequency characteristic.
So, for example, the main tone sets the Universe of ether, the second overtone sets the Universe of star nuclei... the 11th overtone sets the Universe of stars and galaxies... the 120th overtone sets the physical matrix of a human being. The question arises: how and through what do these layers interact with each other? The most common for all layers is the layer of ether, i.e. the maximon medium through which gravitational and, apparently, all other influences are transmitted. In general, the problem of the interaction of different overtones is a very complicated and extremely interesting question.
Another question: can objects of one layer move to other layers? If, for example, stars belong to the 12th layer (11th overtone), can they move above or below?
It is known that stars die after exhausting their internal energy source. In particular, for stars with masses greater than two but less than ten solar masses, astrophysicists have calculated such a scenario: the star explodes, forming a supernova, in which the shell explodes in space, and the core is compressed to a superdense state. At the same time, the structure of all atoms in the core is destroyed, their electron shells are crumpled, and only bare nucleons remain.
The resulting structure is a neutron star, which is a giant nucleus. The NS has dimensions of about \(10^7\) cm, and its elements are \(10^{-13}\) cm. Such a structure belongs to the second overtone (see Fig. 2.42), and since the original structure (a living star) at least belonged to the third overtone, the death of the star is its transition from higher harmonic levels to lower ones. This conclusion returns us to the earlier observation (see Fig. 2.33) that birth is concentration on the S-axis, and death is deconcentration. Now we can say that CONCENTRATION IS A TRANSFER FROM LOWER HARMONICS TO HIGH HARMONICS (Fig. 2.44), and vice versa.
This large-scale scheme reveals to us a deeper meaning of the phenomena of birth and death. THE DECREASE OF OVERTONE LEVEL IS THE PROCESS OF DEATH, THE DEATH OF ANY SYSTEM OF THE UNIVERSE.
Obviously, this follows the mirror conclusion that OBERTON LEVEL BUILDING IS A BIRTH AND DEVELOPMENT PROCESS.
VITIES OF THE SYSTEM. Let us see whether this conclusion has any correspondence to the facts.
Once again, let's return to "Grains of the World Spirit," which consists of the world's ether.
The whole logic of the scale-harmonic model shows that the lower the overtone level, the longer the life span of its systems.
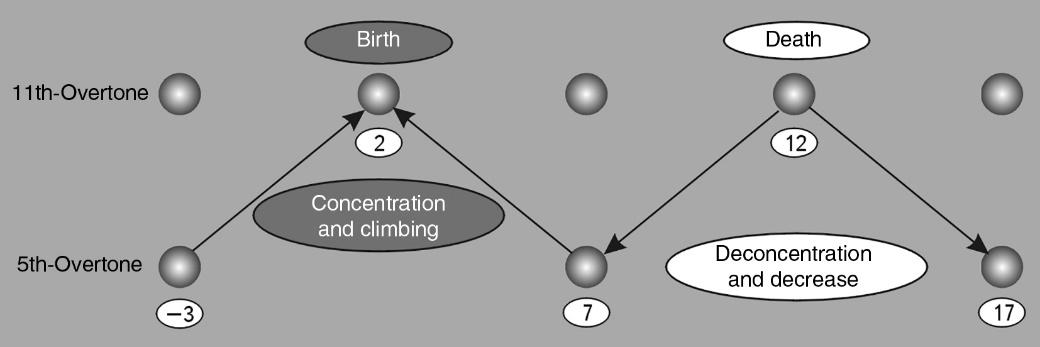
Fig. 2.44. Conditional scheme of birth and death on the diagram of scale-overtone levels. On the right is the death of a star. In this case, it is shown that the separation of a star (+12) into a core (+7) and a shell (+17) leads to a decrease in the overtone level.
On the left is the birth of a human being. It is shown that the growth of the embryo (-3) due to the Biosphere substance (+7) leads to the increase of the overtone level and the appearance of a human being (+2). Of course, the above examples only schematically convey the general idea and do not pretend to the accuracy of modeling the process
Thus, if protons and star nuclei (the second overtone) live for billions of years, then maximon and the Universe (the main tone), obviously, longer. In between (the first overtone) are the "Grains of the WORLD SPIRIT". Hence, they are more stable than protons, i.e., they are more stable than ANY substance!
In the Universe of the first overtone, there is nothing yet, except for maximons, of which they could consist. In such a Universe there is not a single proton, electron, stars, planets, or galaxies. In such a Universe there is no matter yet, because matter is traditionally understood as matter consisting of atoms (or at least nucleons), and there are no atoms in the first overtone, there are no photons because photons as particles appear at the 11th overtone.
At the same time, in the Universe of the first overtone, unlike the Universe of the main tone, there are objects of rather large sizes - about 50 microns (these are the very sizes in which life is created). And these incorporeal immaterial formations theoretically have a mind-boggling stability and, consequently, a lifetime. As we hypothesize, their lifetime must be at least as long as the lifetime of the Universe, since they appeared in their pure form at the second harmonic, at the first overtone. If the Universe has existed for 14 billion years, then its age is the same. And as long as the Universe exists, they will also exist, being an integral part of its life.
Finishing this section, we note that a great variety of the most diverse facts collected by the author during 25 years of research on this question, confirm the reality of scale (four-dimensional) harmony. Long years of phenomenological processing of many reference data on the sizes, scale dynamics, and evolution of various systems of the Universe allowed us to identify and formulate the basic principles of the scale symmetry of the Universe.
All these years the author intuitively felt that behind this large-scale order, there is one simple and rather beautiful principle. Only recent years have given me the confidence that allowed me to formalize this intuitive model and to decide to give an explanation of the hierarchical order with the help of the model of four-dimensional harmony of the Universe.
It turned out that it is necessary to make only one but very fundamental step from the three-dimensional model of the world space to the four-dimensional one, as it turns out that the whole structure and dynamics of the Universe can be described with the help of the theory of waves and oscillations, with the application of the principles of musical harmony. If with the help of the theory of waves and oscillations, we can obtain all the stable dimensions of the evolutionary spectrum, which at the same time is continuously rearranged in its fine details, then the question arises, where do all the spectra of the basis series, which remains unchanged in the whole history of the Universe development, come from?
-
Sukhonos S. I. On the Causes of the Emergence of Preferred Sizes of Natural Bodies in Nature. Dep. VINITI from 27.01.1988. № 733–V88. ↩
-
Sukhonos S. I. The Fourth (Scale) Dimension. (Manuscript). ↩
-
Vladimirov Yu. S. Space-Time: Explicit and Hidden Dimensions. Moscow: Nauka, 1989. ↩
-
Sukhonos S. I. On the Threshold of a Four-Dimensional Civilization // Integral Knowledge. Logos of the Universe. First Issue. Moscow: White Alves, 1999. P. 5–32. ↩
-
Sukhonos S. I. Russia in the XXI Century. Moscow: Agar, 1997. ↩
-
Müller H., Sukhonos S. I. The Law of Densest Packing on All Degrees of Freedom of Biospace // MOIP Reports 1982. General Biology. Experimental Analysis of Functions of Biological Systems. Moscow: Nauka, 1985. P. 98–102. ↩