The S-order of the universe
More than 100 years ago, M. Planck in his report at the meeting of the German Academy of Sciences first proposed the so-called Planck quantities [^note-1], in particular the Planck length, which has since become famous:
$$ l_p = \sqrt{\hbar \cdot G / c^3} \approx 10^{-33}\text{cm} \tag{1.1}\label{eq1} $$ where \(\hbar\) is Planck’s constant, \(G\) is the gravitational constant, \(c\) is the speed of light.
This size is a certain maximum permissible minimum size on the scale the laws of physics known to us are still valid. Penetration into the structure of matter deeper is either impossible at all, or requires the creation of new physics, or will lead to getting into another universe similar to ours (see, for example, the work of Moisey Alexandrovich Markov2.). In any of these variants, the Planck length is the fundamental lower boundary of our world.
On the megascale side, the penetration of astronomy into more and more remote corners of the Universe has led to the fact that it was possible to see the boundaries of the Metagalaxy at distances of the order of \(10^{28}\ cm\). True, in the theoretical model of the Big Bang, the distant boundaries of our Universe are an order of magnitude farther away - about \(10^{28}\ cm\). So, in the twentieth century science has managed to push the large-scale boundaries of our world by many orders of magnitude.
In doing so, it turns out that our world is limited in scope. If there are any boundaries, it is certainly extremely curious to know what is in the center between them? What is equidistant from one scale edge of the Universe as well as from the other? In other words, where is the scaled THE CENTER OF THE UNIVERSE?
It should be remembered that the traditional idea of the middle of the world cannot be used here, because we are not talking about the usual spatial cube, in which diagonals intersect in the center. The question is posed in a different way. To find the middle between scale boundaries means to choose objects of “median scale,”. i.e. such objects that would be so many times larger than the fundamental length, how many times smaller they are than the Universe itself.
At first glance, there is no physical sense in this search, because there can be a great number of objects with such sizes in the Universe. However, let us forgive our idle curiosity and still determine which objects in the Universe are in the scale center of its hierarchical structure. It is very easy to find the scale center. For this purpose, it is enough to construct a logarithmic axis of the sizes of the Universe objects (in principle, it is indifferent what logarithm base we will take, though for calculations it is more convenient to take the base ten), to postpone on it the boundaries of the Universe in microcosm and megamir and to divide the obtained segment in half (see Fig. 1.1). The point in the center of this segment has a value of \(10^{-2.3}cm\) or \(5\times10^{-3}cm\), i.e. about fifty microns.
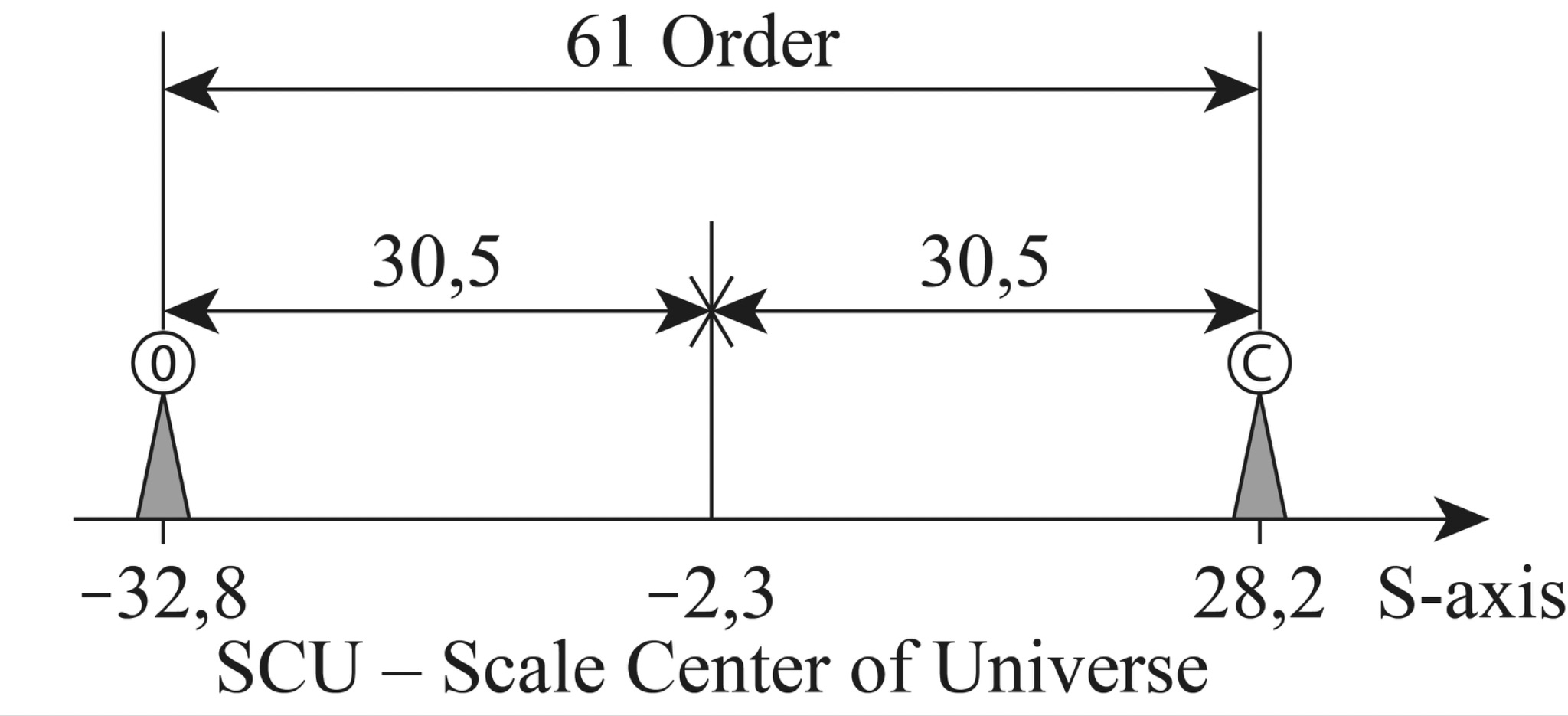
Fig. 1.1. Scale interval of the sizes of the Universe objects (from the fundamental length of M. Planck - \(10^{-32.8}\ cm\) to the visible boundary of the Metagalaxy - \(10^{28.2}\ cm\)) located on the scale axis (S-axis) and its the Scale Center of Universe (SCU)
The obtained value, firstly, pleases with its accessibility (such objects can be seen in an ordinary microscope), and secondly, surprises with its accuracy. After all, the boundaries are God knows where! One - beyond the capabilities of telescopes, another - at the very bottom of the microcosm, and here - 50 microns. Already 5 or 150 microns is far enough from this point.
Therefore, it is interesting to determine what objects common in natural nature have sizes of this order. In inanimate nature, it is the size of dust particles and grains in minerals, i.e., seemingly nothing special. In animate nature, in this selected central place of the whole scale interval of our world there is a biological cell in its geometric mean size (see Fig. 1.2). It is important to note that this geometric mean size is applicable to all kinds of nuclear cells: unicellular, plant and animal. Moreover, the germ cells of most living beings, regardless of their size, have approximately such dimensions. For example, the cell of a fox, a field mouse, a mosquito, an elephant and… a human cell after its fertilization, each of us starts our way into this visible world from the large-scale center of the Universe!
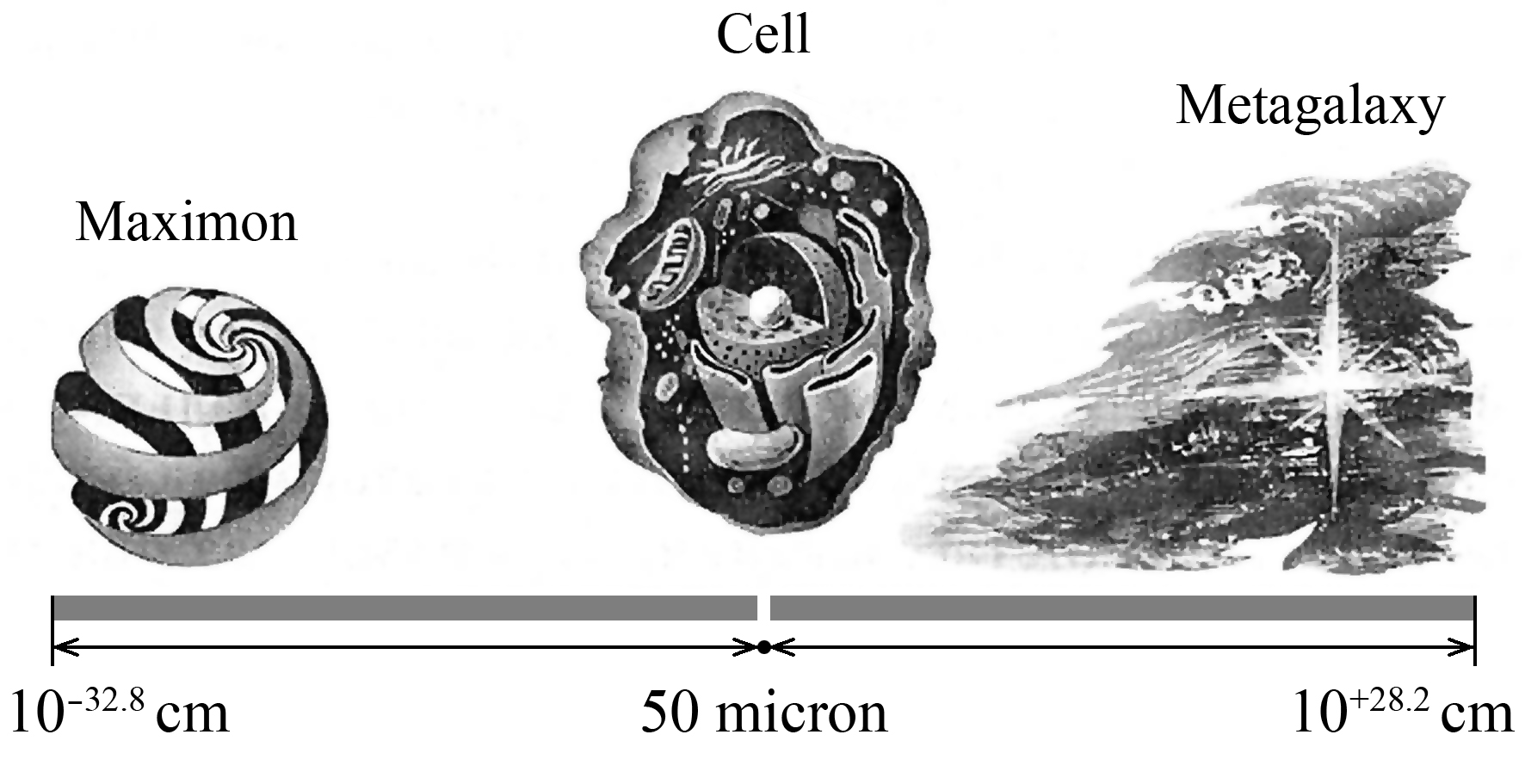
Fig. 1.2. Scale boundaries of our Universe are such that exactly in the center of the scale interval there is a living cell, which is so many times larger than the smallest particle of the Universe - the maximon, how many times smaller it is than its upper boundary - the Metagalaxy
So, using only the well-known data of astrophysics, we get a completely unexpected and intriguing result: In the SCALE CENTER OF THE UNIVERSE (SCU) there is a LIVING CELL - the FOUNDATION of ALL LIFE ON EARTH.
Taking into account the gigantic scale interval of the Universe - sixty one orders of magnitude, there is no reason to consider this scientific fact as a consequence of blind chance. Keeping in mind that we inherit the overwhelming majority of information about our organism, our character, appearance and, most likely, our destiny, we can confidently assert that a genetic person “passes” from generation to generation through a “narrow neck” of a large-scale channel with a “cross-section” of about fifty microns. At the same time, our hereditary “I” stored in each cell is always located exactly in the scale center of the Universe!
So, the central size of the scale range of our world belongs to the living cell, which is so many times larger than the fundamental length in how many times smaller it is than the Metagalaxy. This is hardly an accidental fact, but rather a KEY to the understanding of life in the Universe.
However, to make a final conclusion, we have to make a fascinating journey into the world of new patterns for science, to discover many previously unknown symmetries. We will have to make a long journey into the world of large-scale regularities. And in order not to succumb to the temptation of attributing reality to those regularities that do not exist in it, we will firmly adhere to a simple rule: to use only repeatedly verified scientific facts and data, to rely on such a factual basis, which is virtually no longer questioned in science. Let’s get back to the large-scale range. If we speak about reliable, verified by experiments and observations boundaries, then all our visible world (from proton to Metagalaxy*) is contained within the size range from \(10^{-13}\) to \(10^{27}\) cm, which is exactly FORTY ORDERS (13+27). If we take into account quite probable and most often recognized theoretical boundaries of the scale of our world, it is necessary to consider already 61 orders of magnitude (from \(10^{-33}\) to \(10^{28}\) cm - from the maximon to the Metagalaxy). But if we take into account the fact that over sixteen billion years the expansion of the Metagalaxy has continued, then beyond sixteen billion light years extends a region twice as large, which suggests the existence of invisible boundaries of the Metagalaxy of almost \(10^{29}\) cm.
* In experimental physics it was possible to penetrate only to the depth of \(10^{-17}\) cm, but the reliable boundaries of experimental study of our world are the scales of nucleons - \(10^{-13}\) cm (proton, neutron). Therefore, the author warns in advance that all conclusions, schemes, and models which in this paper refer to the range \(10^{-33}\)… \(10^{-17}\) cm are extrapolations.
In this case, the entire range on the S-axis must be increased to a value of 61.8 orders of magnitude. What lies beyond this interval is a purely theoretical question, and its study often leads to paradoxical conclusions (see, in particular, M. A. Markovs’s model of the “Micro-Macrosymmetric Universe”3). We set ourselves a different task: to see how the internal ladder of the Universe scale is organized, on the steps of which elementary particles, atoms, cells, animals, planets, stars, galaxies, and their all kinds of compounds and systems are located. To look with the purpose of finding out whether the large-scale order of the world order exists or does not exist. At first glance, this question is devoid of any scientific sense - so different systems are juxtaposed against each other. That is why only in popular scientific works sometimes there are pictures (see, for example, the book by B. A. Vorontsov-Velyaminov4), on which the scales of atoms, molecules, cities, solar system, galaxies, and other objects are compared. These pictures are intended to make the novice scientist realize that the range of sizes of objects studied by science is enormous, and partly for this reason each scale slice of our world requires a separate study. It is true that science once encountered a strange scale order, which is difficult to give any explanation, but which is also impossible to ignore. Back at the beginning of the century, Arthur Eddington and Paul Ehrenfest discovered a unique large-scale regularity: it turned out that a reasonable combination of various cosmological constants results in the same dimensionless number close to \(10^{40}\) or its multiple. This problem attracted the attention of all famous physicists, such as Einstein, Gamow, Dirac, and other scientists who dealt with the worldview problems of the Universe structure. It turned out that the obtained result did not follow from any theory, and many years of attempts to find an explanation for it showed that it could not be deduced from any known physical theory.
The problem is called the “BIG NUMBER PROBLEM”. It consists in the fact that there are mysterious numerical coincidences of some dimensionless numerical relations composed of atomic constants, the speed of light and the following cosmological constants: the age of the Universe tp , the radius of the Universe Rp , the average density of matter in the Universe ρp, and the gravitational constant G. It turned out that various meaningful combinations of these constants give surprisingly the same dimensionless value:
Strengths:
$$ \frac{\text{Coulomb (proton-electron)}}{\text{Gravitational (proton-electron)}} = \frac{{e^2}/{r^2}}{{{G}\cdot{M_p}\cdot{m_e}}/{r^2}} = \frac{e^2}{{G}\cdot{M_p}/{m_e}} = 0.2 \cdot 10^{40} \tag{1.2} $$
Lengths:
$$ \frac{\text{Radius of the Universe}}{\text{Classical electron radius}} = \frac{R}{\frac{e^2}{m_e c^2}} = 3 \cdot 10^{40} \tag{1.3} $$
Masses:
$$ \frac{\text{Mass of the observable universe}}{\text{Proton mass}} = \text{number of nucleons} = \frac{{\rho_p}\cdot{R^3}}{M_p} = \left(0.24 \cdot 10^{40} \right)^2 \tag{1.4} $$
At density:
$$ \rho_p = 7 \cdot 10^{-31}\text{g/cm}^3 \quad \text{(modern estimate)} $$
Time:
$$ \frac{\text{Age of the Universe}}{\text{Elementary unit of time}} = \frac{t_p}{{e^2}/{({m_e}\cdot{c^3})}} = \frac{10^{10}\text{years}}{10^{-23}\text{seconds}} = 3 \cdot 10^{40} \tag{1.5} $$
As we see, the scale interval of forty orders of magnitude, which stretched from the proton to the Metagalaxy, is peculiar not only to the ratio of sizes, but also to the ratio of masses, forces, and times. For some time these incomprehensible ratios remained the subject of a separate study. In the 1930s, they were paid close attention to by Paul Dirac, who realized that they are not accidental but show a deep connection between cosmology, gravitation, and electricity. He hypothesized that physical constants change with time, and formulated the following postulate - Dirac’s PRINCIPLE:
Any two very large (about \(10^{40}\)) dimensionless physical quantities are related by a simple mathematical relation in which the coefficients are quantities of the order of one.
Since the relation (1.5) also obeys this principle, which includes the age of the universe, then the question immediately arose:
-
this principle was always valid in the Universe, but then the cosmological and atomic constants must change taking into account the changing age;
-
this principle is fulfilled only in a small period of time of the Universe’s existence, and then we live in some special allocated moment of its development.
To test the first version, astrophysicists conducted theoretical studies aimed at finding the answer: are physical constants constant? A positive answer was obtained with very high precision6.
However, during the test another paradox was revealed: it turned out the most insignificant changes of physical constants lead to the fact that the whole Universe turns out to be completely different. This led to an obvious conclusion: all constants were “selected” in such a way as to produce a Universe in which life, including human life, may have appeared. An important consequence of this conclusion is that all the constants of our Universe have not random values, but are strictly linked to each other through an currently unknown astrophysics law of their harmonization.
Scientists’ discussion of these results has led to two opposing theories:
- THE HYPOTHESIS OF MULTIPLE UNIVERSES (in particular, it is developed by Brandon Carter7). According to this hypothesis, there is an almost infinite number of universes.
All of them are different, and physical constants in them take any value. Only in one of the universes, due to a coincidence of circumstances, the constants took such a value that life could arise.
- HYPOTHESIS OF GLOBAL UNITY OF ALL PARAMETERS OF THE UNIVERSE (in particular, it is developed by John Wheeler). According to this hypothesis, the Universe is one, but in it the global and local laws of evolution are pulled into one tight conceptual knot, which allows Wheeler to ask the following question8:
“AREN’T HUMANS INVOLVED IN DESIGNING THE UNIVERSE IN A MORE RADICAL WAY THAN WE’VE THOUGHT SO FAR?”
The problem of linking the physical constants of our world with the possibility of human existence has so excited the scientific world that the BIG NUMBERS PROBLEM, which actually gave rise to it, has fallen into the shadows and has been on the periphery of attention. It remained an unsolved phenomenon of nature and is only rarely mentioned in review cosmological works.
In the seventies, knowing absolutely nothing about this problem, I set myself a very bold worldview task: to determine whether there is any independent order of structure in the large-scale hierarchy of the Universe.
Since the order can be determined only on the basis of quantitative criteria, it was necessary to choose a parameter that would be universal and peculiar to all systems without exception. Time, mass, forces, size and other parameters were considered by me for their universality and availability. It turned out that the most complete information about all objects of the Universe without exception refers to their geometrical characteristics, and in the simplest form - to their sizes (wavelengths, etc).
First, all real objects without exception have dimensions, and it is this parameter that can be used to compare them with each other. This approach, by the way, agrees with the position of such physicists as J. Wheeler and Dmitri Blokhintsev, who believed that all physics can be reduced to geometry. In particular, D. Blokhintsev wrote: “…the laws of geometry are the most general and extend their power and significance to any events and phenomena in the world that we know.“9
Second, most of the most common objects of the Universe at all levels of its organization have very stable sizes. Therefore, the comparison of objects just by their sizes can lead to quite reliable and sustainable conclusions.
Third, all field processes can be estimated from their wavelengths.
Fourthly, if all objects and processes in the Universe are united by a common harmonic principle, then it is obliged to manifest itself through the distribution of objects by size and the distribution of field relations through wavelengths. If there is no harmony in the Universe, then chaos must reign in the arrangement of all objects on the scale.
Using the most common reference data on the sizes of the objects of the Universe, I began to gradually place them on the scale of decimal logarithms (S-axis), and here a striking regularity appeared: it turned out that the most typical objects of the Universe occupy in their average sizes on the S-axis places strictly through \(10^{5}\). Moreover, many key system properties of the Universe objects (structural and dynamical) have similarity with coefficients \(10^{10}\), \(10^{15}\) and \(10^{20}\). These results were first reported at the First Conference on Classification Theory in Borok in 1979 and published in the popular science journal “Knowledge is Power10. Then two more publications 11, 12 followed, which summarized the main regularities of the discovered phenomenon. Let us now consider the revealed regularity in more detail.