Periodicity of the S-structure of the Universe

At present, the system with the largest size that is accessible to direct observational measurement is the Metagalaxy. Based on the age range of the Universe, according to the references found in the cosmological literature (10–25 billion years), we can accept with some inaccuracy the minimum size of the visible Metagalaxy as 1.6 x $10^{28}$ cm or $10^{28.2}$ cm.

From the other edge of the scale in our world, the minimum (determined experimentally) size has such a well-known system as the proton - 1.6 х $10^{-13}$ cm or $10^{-12.8}$ cm. However, since even in experiments it was possible to penetrate several orders of magnitude deeper, theorists have raised the question: is there any limit at all to the splitting of microparticles into their constituent parts? Quantum theory, relying on the totality of its knowledge, has deduced a certain theoretical limit of matter splitting into elements - this is the so-called fundamental length. Its properties are such that any smaller particles—if they exist—are no longer subject to the laws of our world, and cannot be described by modern physics. We will not go deep into this area of physical theory, since it has its own specificity. Let us only note that some hypothetical microparticles (they were called differently: maximon, plankeons, freedmons, etc.) can have exactly this fundamental size. The exact value of the fundamental size is determined from formula (1.1):

$$ l_p = \sqrt{\hbar \cdot \frac{G}{c^3}} \approx 1{,}6158 \cdot 10^{-33}\text{cm}, $$

or $10^{-32{,}8}\text{cm}$.

The properties of these particles are such that under certain conditions a whole Universe similar to ours can be concentrated inside each particle (M. A. Markov assumed this based only on the known laws of physics). On the other hand, our Universe can be a maximon of the metauniverse of the next level (see Fig. 1.3).

Thus, if we stay within the framework of the world of phenomena we study, we can consider with a certain degree of convention that on the dimensional scale of decimal logarithms¹ our visible world is enclosed in the range of 61 orders: from the Maximon to the Metagalaxy (32.8 + 28.2 = 61).

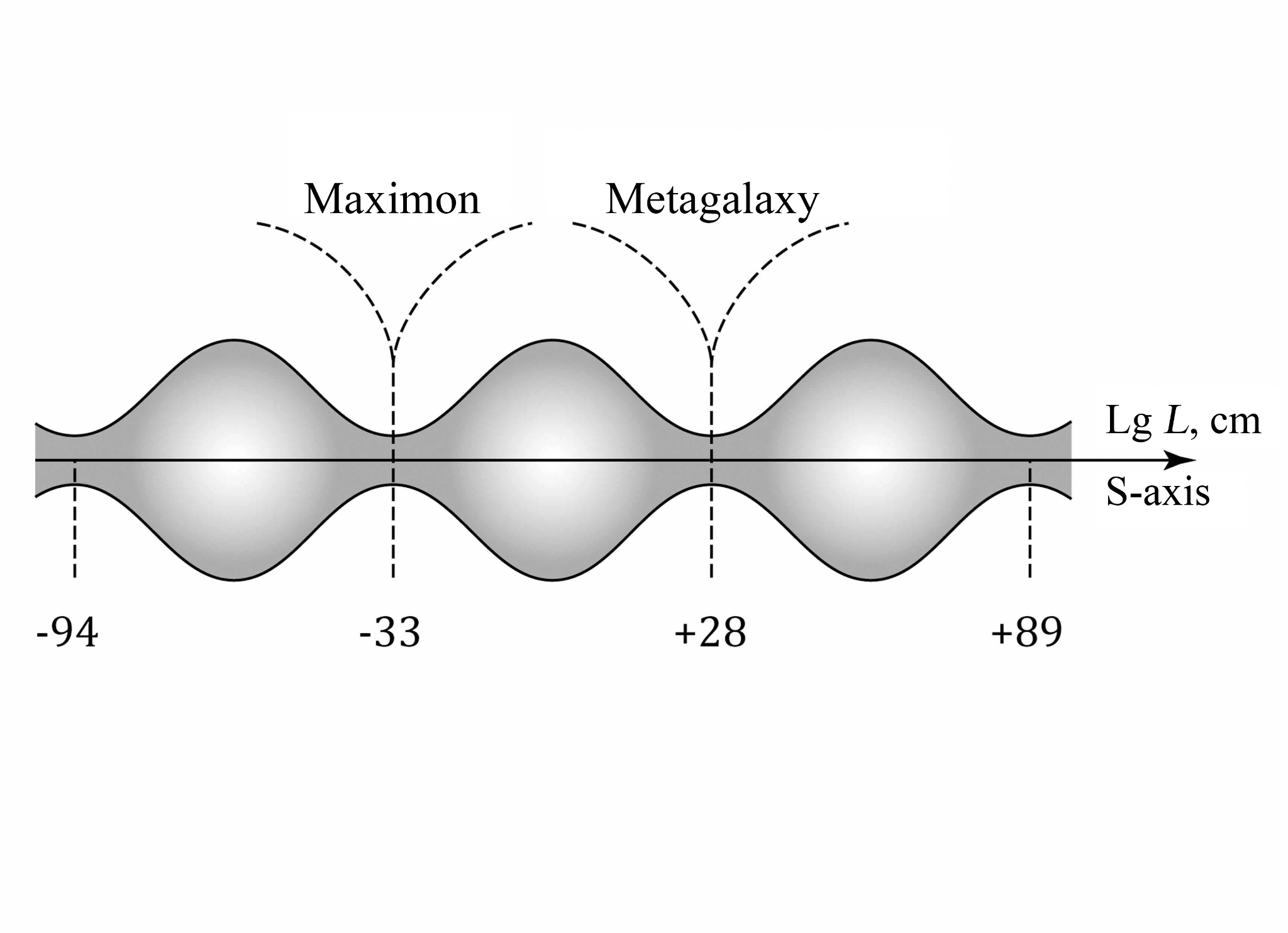
Fig. 1.3. Scale-cyclic model of the world according to M. A. Markov.

Our universe according to this model is just one link in a long (possibly infinite) scale chain of universes

Let us now see how the most well-known and widespread systems are located on this scale. As such, I have chosen the following series:

 0 - Maximons
 
      ...

      4 - protons, the nuclei of atoms,

           5 - hydrogen atoms,

                6 - living cells, 

                     7 is a human being,

                          8 - the nuclei of stars, 

                               9 - stars,

                                    10 - galactic nuclei, 

                                         11 - galaxies,

                                              12 - Metagalaxy.

Let us justify the choice of such a series. First, 99% of the matter of the Universe is concentrated in stars13, which are almost all assembled into galaxies. Stars more than 70% by mass consist of hydrogen, the core of which is a proton. Taking into account the fact that hydrogen exceeds 90% of the content of other atoms by the number of elements of the Universe, and the proton is the longest-lived particle of the Universe ($\sim 10^{56}$ years) - the choice of these objects at scale levels was determined by their overwhelming abundance. The choice of a cell and a human being is subjective only at first glance. Taking into account the fact that the whole science is the activity not of elephants and insects, but of man - the place of man in this row is at least of some interest. Accordingly, man, like all multicellular organisms, is composed of cells. Moreover, according to many biologists, the cell is the most important and representative biological system of the Biosphere.

It is known that the nuclei of atoms determine the basic properties of atoms themselves, although they are in 100 000 times smaller in size. However, not everyone knows that similarly in the megaworld it is the nuclei of stars and galaxies that determine their basic properties, and their sizes are about as many times smaller than the stars and galaxies themselves. That is why the nuclei of stars and the nuclei of galaxies are chosen to build the classification scheme.

The sizes of the proton and the hydrogen atom are known to science to within a tenth of a factor before the power of ten. The average human height has fluctuated in the history of human formation, but still within fairly narrow limits. The sizes of cells, nuclei of stars, nuclei of galaxies and galaxies themselves were determined by me as geometric averages by the same procedure. If, for example, it is known that stars do not occur less than $10^{10}$ cm and more than $10^{14}$ cm, then the average size of a star was defined as a point on the scale equidistant from these limits, i.e., $10^{12}$ cm.

The author's detailed studies of this question have shown that with an error of up to 10% (0.5 orders of magnitude on the scale of decimal logarithms) the selected series of systems (including the average sizes of stars, galaxies, etc.) occupy places on the S-axis alternating through 5 orders of magnitude ² (or multiples thereof). The figure 1.4 shows the S-axis and the points where the selected objects are located on it.

This result shows that there is a strict order in the massive hierarchy of the Universe.

A DEFINED PERIODICITY that is not related to the kind of ruler (centimeters, meters, parsecs...) and is defined by a dimensionless relation that can be formulated very simply.

The average galaxy is as many times larger than the average galactic nucleus as the latter is larger than the average size of a star, which in turn is as many times larger than the average size of a star's nucleus, etc,.

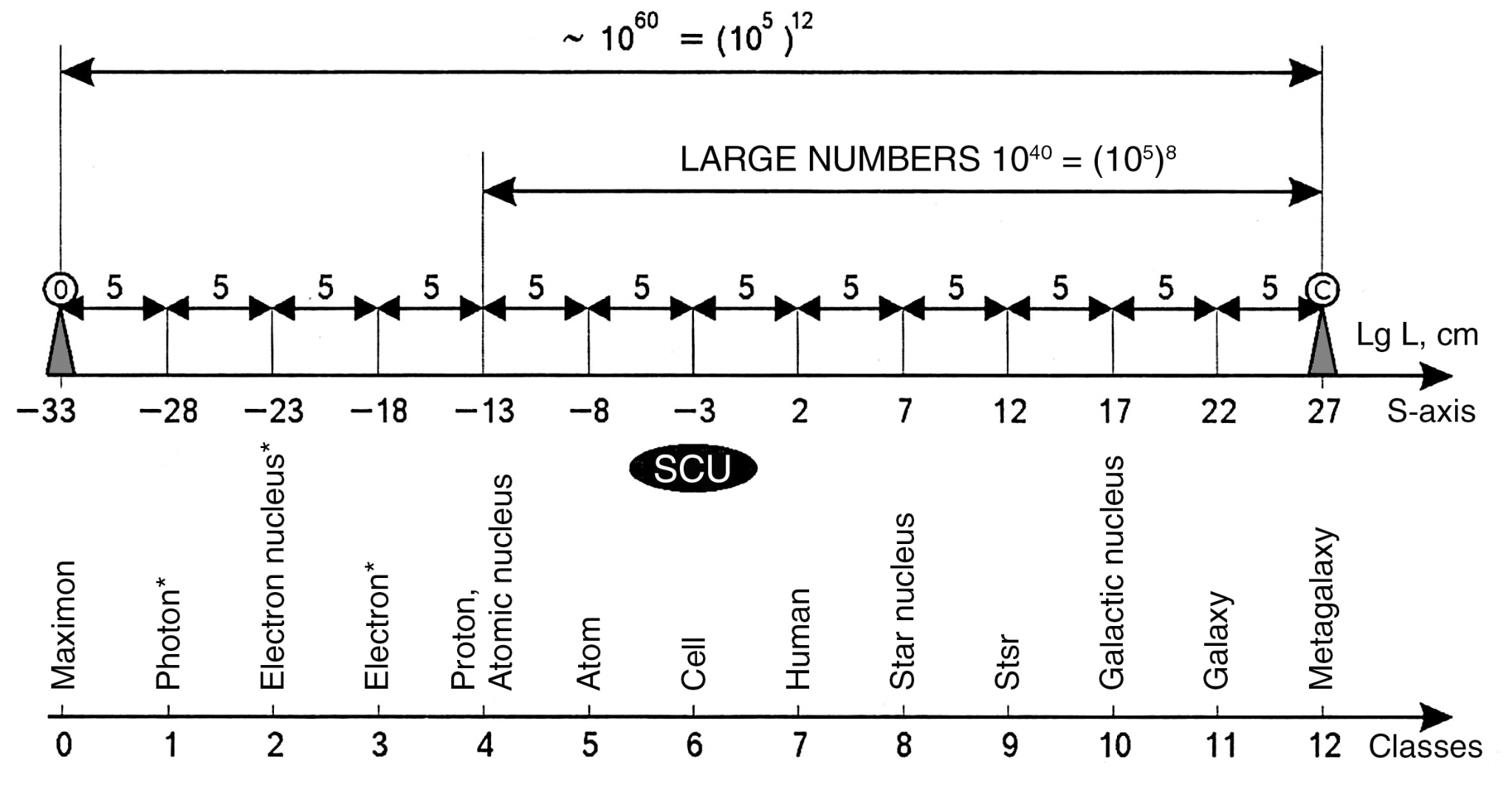
Fig. 1.4. Scale axis of the Universe (simplified model³) divided into 12 intervals of 5 orders each. A shift on the S-axis by one order to the left or right means a 10-fold change in size

Let us return to the problem of large numbers. We see that this unique regularity is only a fragment of the general regularity discovered by the author (see Fig. 1.4).

True, it may seem that the pattern of LARGE NUMBERS has a more general status, since it exhibits regularities in several parameters rather than in single dimensions. The author's preliminary study, however, has shown that the discovered dimensionless periodicity with a prime factor of $10^{5}$ is peculiar to all the main parameters of the Universe: times, masses, forces, etc. The fact that the main representatives of the MASHABLE classes ⁴ of systems are located on the S-axis strictly periodically, with a period that does not change during twelve operations of its postponement from the leftmost point, and the accuracy is more than 10%, testifies to the presence of strict orderliness in the scale hierarchy of the objects of the Universe. Although we can currently judge the values of the average sizes of such objects as the nuclei of stars and the nuclei of galaxies with a low degree of accuracy, our study shows that, with further refinement of the sizes, the accuracy of their coincidence with the model sizes (taking into account the revealed bimodality in the distributions14) only increases.

Let us show by concrete examples how the sizes of objects with a five-order period coincide.

SCALE CLASS #0. The leftmost point of the scale interval - the size of the maximon (fundamental length) is theoretically determined with a very high degree of accuracy.

$$ l_p = 1{,}6158 \cdot 10^{-33}\text{cm}. $$

SCALE CLASS #4. Exactly after 4 intervals of 5 orders of magnitude, which gives a shift along the S-axis of 20 orders of magnitude, we obtain a value of 1.6 × $10^{-13}$ cm, which is identical to the proton diameter with an error below 0.05 for the factor before the tenth.

So, we have made a shift of twenty orders of magnitude and obtained a point on the S-axis, which with an accuracy of 0.005 of one order corresponds to an extremely important size in the Universe - the size of the most common and long-lived particle - the proton. Consequently, the deviation of our calculated size from the real one is less than 1/20000!

However, the deviation can be defined in another way (see diagram on page 43).

SCALE CLASS #5. Another step of five orders of magnitude along the S-axis gives us a size of 1.6158 × $10^{-8}$ cm. According to most sources, the diameter of the hydrogen atom is 1.4 × $10^{-8}$ cm. The deviation from the calculated value is 0.2158 ⁵. At one order of magnitude, the deviation is 10 times smaller ~ 0.02. Given that the shift from the fundamental length is 25 orders of magnitude, the calculation shows an error of 0.04% (0.02: 25 = 0.0004 = 0.04%). The maximum deviation from the theoretical grid is 5 orders of magnitude higher and equals 0.4 %.

SCALE CLASS #6. The next step gives us a value of 1.6158 х 10-3 cm. Approximately this size, as the study of cytology material has shown, does play an important role in the life of cells.

Unfortunately, biology still treats size parameters as illustrative and often does not even indicate the size of certain cells, or if it does, it is very approximate. Therefore, reliable statistics on cell sizes have yet to be collected in order to draw any confident conclusions. We can, however, say that with an accuracy of 1 order of magnitude this value coincides with the average size of all cells. In this case, the calculation error at thirty orders of magnitude does not exceed 1/30, and for the grid it is 1/2.5.

ERROR CALCULATION SCHEME

If we take into account that on the whole scale axis (S-axis) we imposed a periodic scale with a step of 5 orders of magnitude (periodic grid), then the value of the maximum possible deviation of the most important objects of the Universe from the nodal points of the grid will be 2.5 orders of magnitude (the maximum remote point from the selected marks will be in the middle between them).

The points of maximum deviation from the periodic theoretical mesh on the S-axis are shifted relative to the nodes by 2.5 orders of magnitude

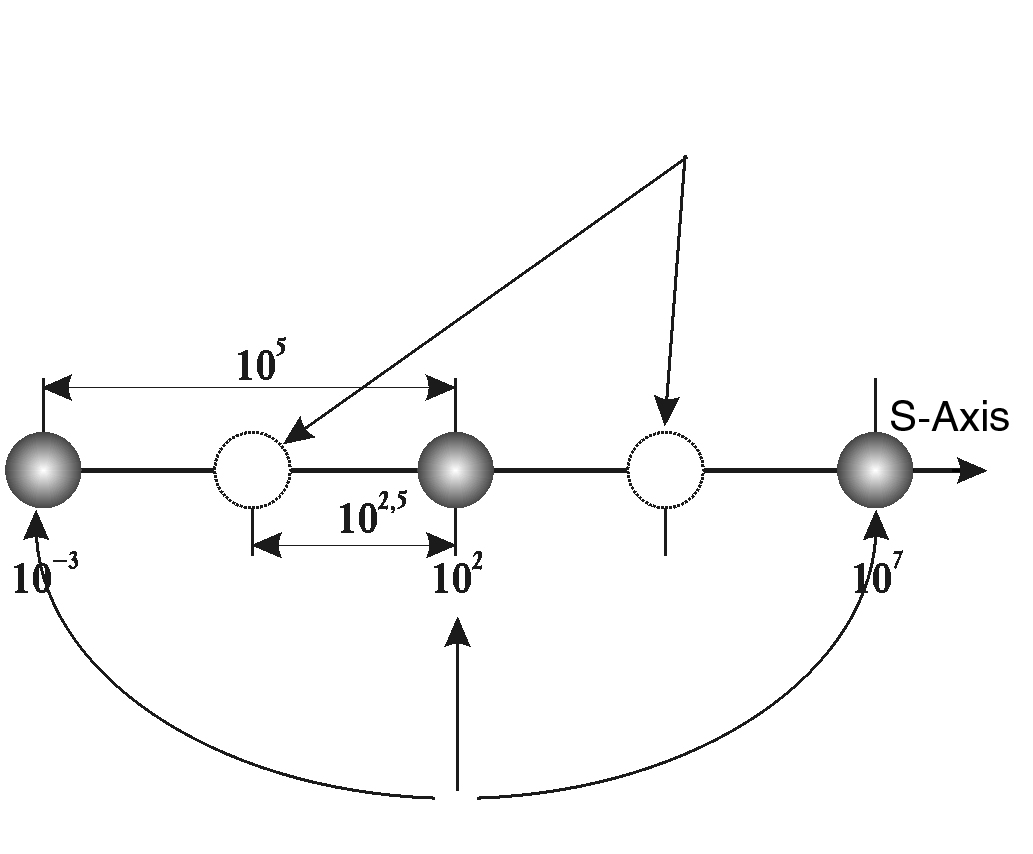
Periodic grid nodes with a step of 5 orders of magnitude

Consequently, the maximum theoretical deviation from the nodes of the chosen periodic grid will be 1/2.5 orders of magnitude, so for the factor before the tens, whose value can run values from 1 to 9.9..., each whole unit of deviation will give an error of 1/25. (For example, going from a size of 5 meters to a size of 6 meters is only a change of about 1/10 of one order of magnitude; for 2.5 orders of magnitude, such a change in size results in a deviation of only 4% (0.1: 2.5 = 0.04 = 4%).

5 × $10^{21}$...6 × $10^{2}$ (5 to 6 m) = 0.1 intervals of 1 order. (One order of magnitude corresponds to a 10-fold increase in size.)

Since the deviation of the proton size from the theoretical value does not exceed 0.05 fermi, the total error in this case can be defined as 0.05:10:2.5 = 0.002, or less than 0.2%. This error is larger than that obtained above, but it is still negligibly small, and given the inaccuracy of determining the proton diameter for values after tenths, it can be neglected altogether.

SCALE CLASS 7. Another step to the right gives us the value 1.6158 × $10^{2}$ cm. The average human height until the beginning of the XXI century was quite close to 1.6 m, in our time it has increased by 4-5 cm (most likely due to hormonal additives to animal food). But it hardly deviates from the average value of 1.62 cm by more than ±10 cm. Therefore, with a large margin of error we can assume that the error is less than ±0.1 m, and this will give us a deviation from the calculated value of 0.02 orders of magnitude. Taking into account that the limit deviation is 2.5 orders of magnitude, the average human height is determined with an accuracy above 0.4%. It is important to note that three known cosmological constants (G, ħ, c) and one discovered by the author, were used in the calculation of the average human height. Let us consider this dimension in more detail. Obviously, the obtained error is so insignificant that the non-randomness of man's growth in the universal hierarchy can be considered strictly proved. If we take into account that deviations could accumulate in the periodic series of sizes (to get to the man, we made 7 such steps, and the deviations were not accumulated, but mutually compensated), and if we take into account that the real average height deviates from the value of 1.6158 meters by less than ±10 centimeters, then the hit of the man's height in the general periodic series of hierarchical floors can be considered simply ideal.

It is impossible to attribute this fact to thoughtless combinations by constants. After all, the fundamental length obtained by M. Planck more than 100 years ago from three physical constants, is considered in science as one of the most important dimensional constants of our world. And the dimensionless coefficient $10^{5}$, derived by the author, is universal for all basic objects of the Universe, with its help a number of dimensions is built, in which the proton, hydrogen, and all other significant objects are exactly located.

Let's assign to the calculated cosmological value of the average height of a man the status of the average Theoretical Universal Human Height ($L_{\text{HSU}}$):

$$ L_{\text{HSU}} = (10^5)^k l_p = (10^5)^7 \cdot 1{,}6158 \cdot 10^{-33} \text{cm} = 1{,}6158 \cdot 10^2 \text{cm} = 161{,}58\ \text{cm} \tag{1.6} $$ where k is the number of scale class, or the number of scale level, for a human it is equal to 7.

It can be assumed that, throughout the entire history of humanity, the average height has fluctuated around or tended toward the cosmological average height. The calculation of the average height of a modern person in different countries is of separate interest.

Let us make a calculation for our country. According to the GSE (The Great Soviet Encyclopedia),, in the USSR in 1960-1970, the average height of men was 167-168 cm, and women - 156-157 cm. It is not difficult to calculate that for the average resident the average height was somewhere in the range of 161.5x162.5 cm. The arithmetic mean is 162 cm. Given that at this time there were about 10% more women in the country, the average value must be adjusted downward. Thus, the average height of the USSR inhabitants in this period differed from $L_{\text{HSU}}$ by less than 4 mm. Taking into account the spread of 1 cm, which accompanies the indication of the average height of a person in the GSE, we can assume that it did not deviate at all from the $L_{\text{HSU}}$ calculated by us!

However, since the first calculation of average human height, it has grown by 4-6 centimeters. Most likely, due to the use of hormones in the cultivation of agricultural products. And it has become more than the calculated theoretical value. But once again we repeat that a deviation of even 10 cm for this value is a negligible error.

Moreover, the obtained calculation is just a first estimate, but these two values - Theoretical Universal Human Height - TUHH and the real average height of the USSR inhabitant - coincide too precisely for this calculation to be just another random coincidence. So, we see that, at least for three objects: the proton, the hydrogen atom and a human being, the accuracy of the periodic partitioning of the S-axis is incredibly high. There arises an assumption that for other systems of the Universe the characteristic sizes of their most representative species have such a high coincidence with the calculated one.

By the way, it is possible to note (see relations (1.2) - (1.5)) that the ratio of LARGE NUMBERS, which so excited all physicists, has an error of more than one order (coefficients from 0.2 to 3.0) at 40 orders, which gives an accuracy not higher than 1/40, i.e. 2.5 %. If the error of 2.5 % did not embarrass physicists in the past, the error of 0.005-0.04 % should not embarrass them in the present study.

SCALE CLASSES # 8, 9, 10, 11. Four more levels were determined from reference data as the geometric mean sizes of stars, stellar nuclei, galaxies, and galaxy nuclei, as already mentioned, with an accuracy of 10 %. In future work, the technique for determining these sizes will be shown in an expanded form.

SCALE CLASS #12. Metagalaxy - estimates of its apparent radius from astrophysical data range from $10^{28}$ cm - 2.5 × $10^{28}$ cm. According to the concept of the finiteness of light, the "edge" of the Metagalaxy that astronomers see is in a position much closer than the real one. Because of the expansion, the real radius of the Metagalaxy can be from 32 light years away, and the diameter, accordingly, can be twice as large and reach a value of almost 6.4 × $10^{28}$ cm. Thus, in different variants it is possible to use the parameters (1.6–6.4) × $10^{28}$ cm.

For further calculations, we will use the value 1.6 × $10^{28}$ cm, or, what is the same, $10^{28.2}$ cm. For the reason that all electromagnetic oscillations have reached us and other corners of the Universe exactly from this distance. In this case, this observational value has a maximum deviation from the model point on the S-axis ($10^{27}$ cm) of about one order of magnitude.

So, it has been found out that the most representative objects of their scale levels are located along the S-axis of the Universe with strict periodicity. However, in this periodicity, firstly, there is a micro-interval (the so-called Dirac basement), the structure of which we have to extrapolate by placing the photon, the electron nucleus and the electron itself on scale shelves, about which modern science cannot yet say anything even in theoretical calculations. And secondly, we have occupied two more shelves with bio objects (cell and man), which in the general series of systems of the Universe look like a special (though important for us) case. Thus, in the constructed periodicity of thirteen floors, the existence of five additional floors remains a significant question. In the following we will show that experimental physical data remove completely the question from one of the floors - the sixth, which plays a key role in the thermodynamics of the Universe. However, the other four floors (1, 2, 3, and 7) remain in many respects somewhat predictive.

METHODOLOGICAL DEPARTURE

Before moving on, I would like to consider the question of the methodology of building a periodic scale hierarchy. The point is that any continuous scale sequence of systems of the Universe will be perceived naturally if it has a constant transition factor of the type "consists of..." or "is included in...". For example, the Metagalaxy "consists of..." galaxies that are not observable outside of it, so all galaxies are "included in..." Metagalaxy. Further, any galaxy "consists of..." stars, and vice versa, no galaxy-free stars have yet been found. Stars themselves are made up of atoms. True, atoms may well exist outside stars. However, on the other hand, these extra-stellar atoms in the Universe are so few (less than 0.1%) that they can be neglected and the opposite phrase can be written: atoms are "included in..." stars. Atoms are also "composed of..." protons, neutrons, and electrons, and we can confidently assume that most of these particles are not "walking around free" but are "included in..." atoms. Further, the particles are apparently "composed of..." maximon.

Thus, we have a continuous series of systems, which are very rigidly connected with each other by the system of mutual inclusion. In this series, as it has already been noted, there are relations of scales of type $10^{5}$ or multiples of it. At the same time, if everything is practically obvious for the micro and megaworld, for the macro-world we encounter a serious methodological problem. We cannot claim that stars are "composed of..." people (although the priests of ancient Egypt believed so). However, further everything is in order: a human being consists of cells, cells consist of atoms.....

It is very difficult to find a way out of this PARADOX (which we ourselves, by the way, created) today. After all, if we consider the Earth with all its inhabitants to be a small side branch (in terms of mass) on the giant scale trunk of the Universe, then all its objects are a very private aspect of the Universe structure. The main "trunk" in the interval from atoms to stars is simply not yet studied by science. Due to purely natural and methodological difficulties, astrophysics is not able to study structures with dimensions of the order of interest not only in stars, but even in the Sun. Therefore, science cannot assert both that there are any distinguished and stable structures on this scale interval and that there are none at all. In this case there are no prohibitions on some model fantasy and we can assume that stars "consist of..." some not yet discovered, but very stable subsystems, the sizes of which are on average $10^{5}$ times smaller than their own. This, by the way, is quite confirmed by the surface structure of the Sun (the average size of the star is approx. $10^{12}$ cm), the "granules" of which have an average order of magnitude of approx. $10^{7}$ cm. The "granules" themselves according to our scheme should also consist of some very stable structures of meter sizes, which are still five orders of magnitude smaller than themselves. It is clear that it is currently impossible to see such structures on the surface of stars, not just stars, but even the Sun. An even more incredible task is to verify the thesis that these meter-sized parts of "granules" should "consist of..." quasi-cells with sizes of tens of microns.

So, since astrophysics has not yet revealed anything similar even in the structure of the Sun, we find a gigantic failure of scientific information about the macrostructures of the most common systems of the Universe - stars. It turns out that observations do not give us any information about the structures in the size range from the scale of atoms to the scale of stars.

If we follow classical ideas, stars are composed of atoms (and their ions). Consequently, from stars to atoms in our series of systems through five orders of magnitude we practically cannot put with certainty any stable structures. Perhaps they really don't exist, but then there is a giant gap in the scale floors of the Universe (skipping three steps). Perhaps they do exist and play a very important role in the life of stars, but have not yet been detected, so this scale failure is the result of our profound ignorance of the true structure of stars. Once again, recall that stars are 99% of the matter of the Universe, so any studies of this series on Earth alone are curious, but statistically very unrepresentative.

As for my own point of view, I quite admit that the substructure of all stars has all the above-mentioned stable floors alternating through five orders of magnitude. And it is possible to detect them not necessarily directly - visually, but also indirectly, through the regularities of frequency periods, which are surely related to these hypothetical stable sizes.

Summarizing this section, we can note that if we PROVIDE the existence of four-five more selected stable dimensional floors in the Universe, then its entire scale structure will be subject to a strict periodicity. And in some cases it is possible to establish that this periodicity is observed with incredibly high accuracy. If we discard all assumptions, we should note that the gigantic gap in the large-scale periodic structure of the Universe from atoms to stars is filled in our work with a thin web bridge mainly from biological systems of the Earth. It is simply not possible for us to know anything else for today. In order that the reader does not get the impression that this periodicity is peculiar only to the size of objects. Let us give some examples from other parametric domains. Take, for example, a number of characteristic physical and cosmological times. Let us note in advance that any system can theoretically have (and, as a rule, actually has) at least three characteristic times:

t - is the time for a signal propagating at a finite speed (e.g., the speed of light) to traverse the system cross section;
τ - is the time of oscillation of the system relative to the equilibrium point (natural period of oscillation);
T - is the time the system is in the excited state. Let us take ATOMS for starters. It is easy to calculate that an electromagnetic wave passes through the cross section of an atom at a time t of about $10^{-18}$ s ($10^{-8}$ cm / $10^{10}$ cm/s).

The natural period of vibration ($\tau$) of all atoms in condensed media is known to be constant and equal to $10^{-13}$ s.

The lifetime of an atom in the excited state (T) is also known, it is equal to $10^{-8}$ s.

We see that the consecutive ratio between these three most important atomic characteristic times is $10^{5}$. Maybe this ratio is peculiar only for atoms? However, it is not. Let us consider characteristic times for other objects of the microcosm - atomic nuclei.

It is easy to calculate that the electromagnetic wave passes the cross section of the atomic nucleus in time t equal to $10^{-23}$ s = $10^{-13}$ cm / $10^{10}$ cm/sec. This same time is widely known in nuclear and elementary particle physics as the characteristic time of nuclear interactions. Another time, the lifetime of the nucleus in the excited state, T, is also well known. It is equal to $10^{-13}$ s, which is ten orders of magnitude longer than the nuclear interaction time.

In accordance with the regularity established for atoms, we can calculate the intrinsic period of vibration of the atomic nucleus - $\tau$. According to our scheme it should be $10^{5}$ times less than the lifetime of the nucleus in the excited state - $10^{-18}$ s. ⁶

So, we can PROPOSE that also for atomic nuclei the three characteristic times are correlated with the coefficient $10^{5}$. In any case, it is obvious for two of these times.

One can BELIEVE that the time logarithmic axis on this scale interval also has selected points (see Fig. 1.5), which are five orders of magnitude apart. Otherwise, how else can we explain the fact that characteristic atomic times are elementarily obtained from characteristic nuclear times by multiplying them by $10^{5}$?

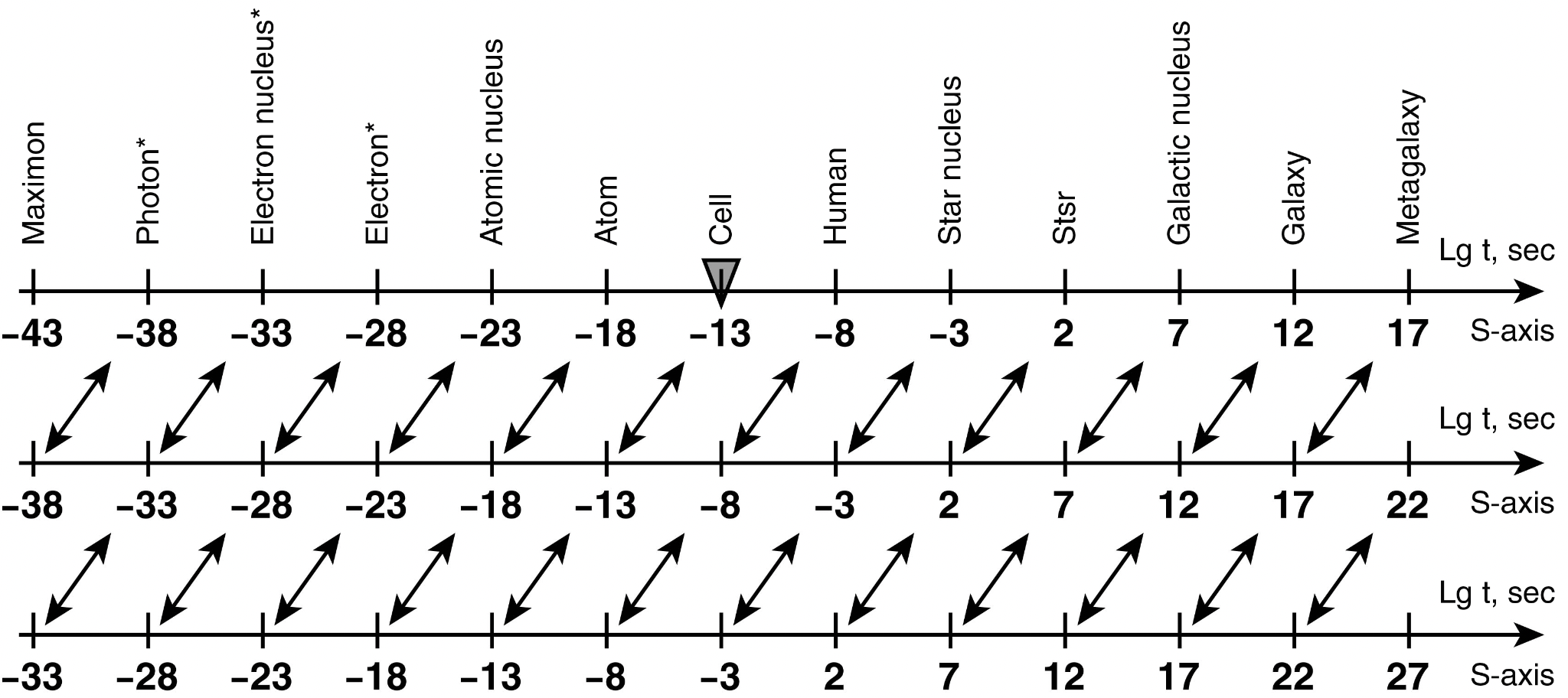
Fig. 1.5 The scale-time periodicity ($10^{5}$) of the Universe assumed by the author (simplified model). ⁷ ⁸

How can we explain the fact that for the Earth's orbit, the dimensions of which are about $10^{13}$ cm, by quadrupling the oscillation period of the atom by $10^{5}$ we get the value: $10^{-13}$ s × $(10^{5})^4$, i.e. about $10^{7}$ s, which is surprisingly close (taking into account the huge distance on the logarithmic axis) to the value of one year (365 × 24 × 60 × 60 = 3 × $10^{7}$ s).

Hence, we can PROVE that on the S-axis the conversion factor of characteristic dimensions into characteristic times is the speed of light.

Further. The coefficient $10^{5}$ can also be found in the relations of field interactions. Thus, the experimentally found constant of the four-fermion interaction, which according to the Fermi model can be considered as a weak interaction, can be written in the form ⁹:

$$ \mathbf{G}_f = 10^{-5} \cdot \hbar^3 / M^2 \cdot c \tag{1.7} $$

where ћ is Planck's constant, c is the speed of light, and M is the mass of the nucleon.

Another example from the field of microphysics. It has been calculated16 that the mass of a boson necessary to realize the so-called grand unification (all kinds of interactions) must be $10^{15}$ times the mass of a proton, which on the mass scale axis corresponds to a threefold multiplication by the factor $10^{5}$.

So, we see that the ratios not only of sizes, but also of other important parameters (times, masses...) of the most representative objects of the Universe often show the same dimensionless coefficient - $10^{5}$.

The facts listed above, related not to the sizes but to other parameters, may seem randomly selected, so the author once again warns that a thorough and complete study of scale periodicity is made by him only for the parameter of the sizes of systems. It is in this area that the choice of each of the points on the S-axis is reasonable, not random. It is worth recalling once again that in recent decades most theoretical physicists have increasingly come to realize the leading role of spatial regularities. There is an intensive work on geometrization of physics.

"Matter is an excited state of dynamic geometry... Geometry predetermines the laws of motion of matter..." ¹⁰

Concluding this section, let us consider in more detail, perhaps, the most intriguing fact established by the author in the course of research into the large-scale hierarchy of the Universe: THE CENTRAL LOCATION ON THE S-INTERVAL OF THE UNIVERSE OF THE HUMAN SEX CELL (see Fig. 1.6A). With incredible accuracy nature literally adjusts to the value close to 30-50 microns the size of the male sex cell and the egg cell nucleus at the moment of their synthesis (see Fig. 1.6B), and it is this size that corresponds to the S-Center of the Universe or SCU, or a point on the S-axis (-2, 3).

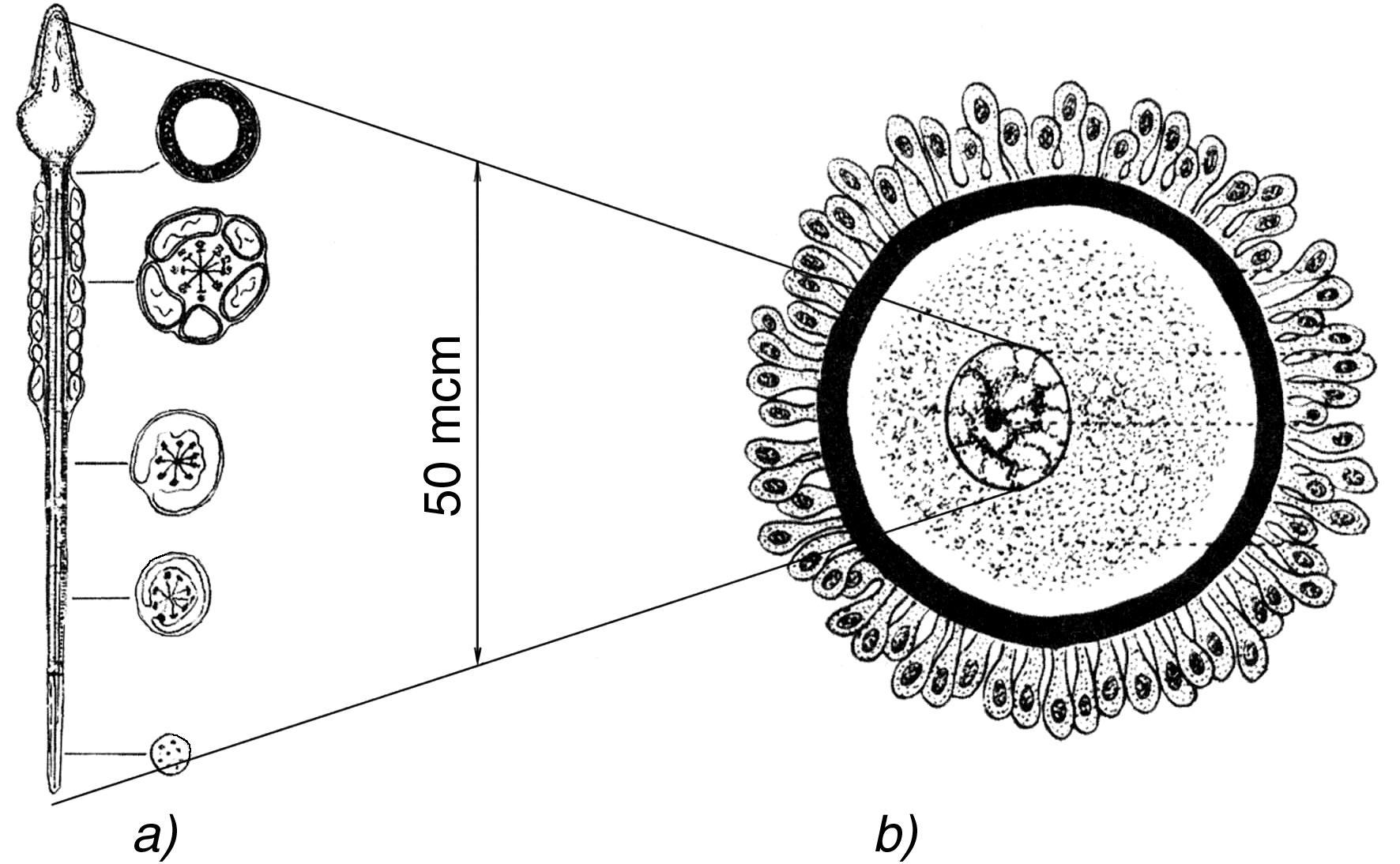
Fig. 1.6A. The sperm cell (a) is 50-60 microns long. The female germ cell (b) is much larger: 130-160 microns, but its nucleus is also approximately 30-60 microns long.

Many years of reflection on this fact have convinced me that it is not a coincidence, but a consequence of a special, allocated position of life and man, especially in the large-scale hierarchy of the Universe. After all, if we consider man in a more generalized plan as a generic man (and there are many reasons for it, for example, such as: more than 80 % of man's life is determined by his genetic heredity, which is formed just in the SCU), then we can confidently assert that man is a QUINTESSENCE of all the processes going on in the Universe, and occupies in its hierarchy an ABSOLUTELY exactly central place.

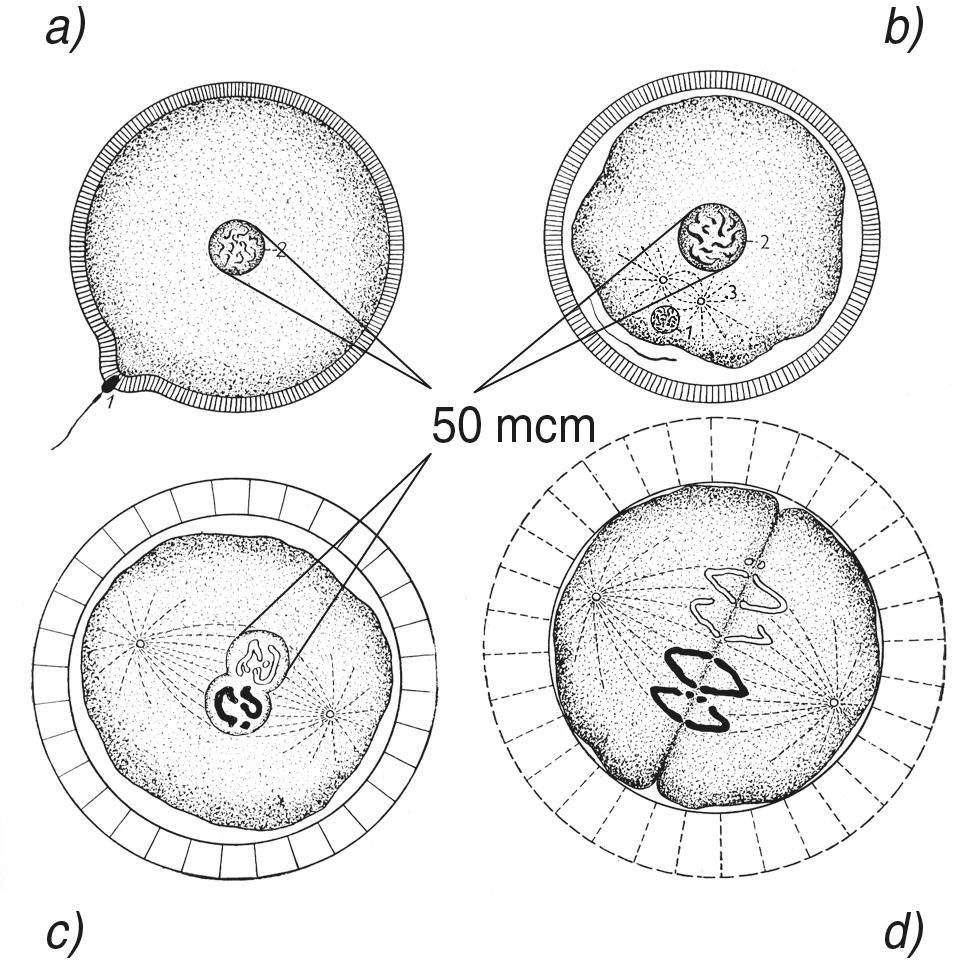
Fig. 1.6B. As a result of the "race", only one of the 200,000,000 sperm pierces the female cell membrane (a) and penetrates it to effect fertilization. The sperm head, which is much smaller in volume than the female primary nucleus, then begins to gradually increase in size (b) until it reaches approximately the volume of the egg cell nucleus and, remarkably, a size of about 30-50 microns. Only then does the contents of both primary nuclei fuse into a common nucleus (c). The synthesis of the nuclear material, which takes place absolutely precisely in the scale center of the Universe, ends the process of fertilization and begins the ontogenetic development of the new organism (d). Thus, the starting scale "site" for each human being is the scale center of the Universe (50 microns), and the finishing "scale line" is the size of an adult organism, which is exactly 5 orders of magnitude higher on the scale scale of sizes.

However, this topic is so important that we will leave it to special consideration.

The choice of the scale of decimal logarithms was determined at the first stages by considerations of convenience, since most of the sizes of the objects of the Universe in scientific literature are given in this traditional form. ↩
The only exception to the established rule is the Metagalaxy itself, which is located on the S-axis 1 order of magnitude to the right of the calculated location. ↩
For simplicity of explanation of the main idea, two models of the scale symmetry of the Universe are used in this paper: a simplified model, or rounded to integer orders, and a refined model using hundredths of an order. The simplified model is convenient for clarification of the basic regularities of scale symmetry, and the refined model is convenient for verification of phenomenological data. At the same time, the simplified model uses the values of the size of the maximon - $10^{-33}$ cm and the size of the Metagalaxy - $10^{27}$ cm (which corresponds to its age of about 1 billion years), i.e., it operates with the S-interval $[-33; +27]$ with a length of 60 orders of magnitude.
The refined model uses size values of $10^{-32.8}$ cm and $10^{28.2}$ cm, respectively, i.e., considers the S-interval $[-32.8; +28.2]$ with a length of 61 orders of magnitude. Such replacement of one interval by another in order to emphasize the reader's attention on the main points of the author's idea gives an error of only 1/60, i.e., only 1.5%. ↩
A clear classification will be given later, see Fig. 1.7. ↩
The reason for this discrepancy may also be some underestimation of the true sizes of atoms, the boundaries of which are determined by the maximum density of the electron cloud. ↩
However, the author has not been able to find a reference to such a time in the literature. Perhaps it is simply rarely mentioned, perhaps it has not yet been discovered. ↩
$10^{17}$ seconds is about 10 billion years - the lifetime of the universe. ↩
Or a planetary orbit, such as Mercury. ↩
Vladimirov Y. S. Space-time: explicit and hidden dimensions. Moscow: Nauka, 1989. С. 97. ↩
Wheeler J. Einstein's Foresight. М.: 1970. С. 15-18. ↩

THE NEW DIMENSION OF THE UNIVERSE

Periodicity of the S-structure of the Universe

ERROR CALCULATION SCHEME

METHODOLOGICAL DEPARTURE