S-similarity of the Universe
The analysis of the previous material suggests an additional hypothesis - about the mutual similarity of the three main intervals of the S-axis with a length of 20 orders of magnitude. After all, if each of them "belongs" to only one force (see Fig. 1.7), it is possible that the laws of action of these forces on matter have a similar character. This may first of all manifest itself in the similarity of the structures of objects belonging to the same parts of the three selected intervals, i.e. in the scale-structural invariant.
This idea first appeared to the author when it was found out that there are objects with similar structures in Macro- and Mega-intervals. First of all, these are atoms and stars. Although the structure of the atom was inspired by Rutherford by the structure of the Solar System as a whole, and not by the Sun separately, the similarity of atoms with stars seemed to the author to be greater.
Indeed, both atoms and stars have a small central nucleus, and they have spherical shells. The most common atom in the Universe, hydrogen, has a spherical shape similar to stars. Astrophysicists are convinced that it is in the cores of stars that the main processes that determine their properties are going on. Atoms are characterized by the dominant influence of the properties of the nuclei on them. Generally speaking, both stars and atoms have a pronounced monocentric structure. However, the solar system (like, apparently, any other system) also has a monocentric structure - the nucleus - the Sun, but still, unlike the atomic system, the structure of the solar system is flat. The decisive factor, however, for me to choose a pair of similar structures was that the average size of stars (\(10^{12}\) cm) is ideally 20 orders of magnitude larger than the size of a hydrogen atom (\(10^{-8}\) cm). When I first became acquainted with the materials on neutron stars1, I was struck by the precision of the similarity even more. After all, neutron stars are made up entirely of naked nucleons. In fact, they are giant atomic nuclei, only they contain \(10^{60}\) times more nucleons. Their size (~\(10^{7}\) cm) is 20 orders of magnitude larger than the size of atomic nuclei (\(10^{-13}\) cm). You can "go around" the entire hierarchical ladder of the Universe up and down many times, but you will not find anything like this on any other scale floor. There are systems of bare, densely packed nucleons (ρ ~\(10^{15}\) g/cm3) only at two scale levels: in atomic nuclei and 20 orders of magnitude higher (to the right along the S-axis) - in neutron stars.
I quickly realized that this could not be a coincidence. Behind this fact there is a large-scale similarity of structure types, similarity with coefficient \(10^{20}\). Checking confirmed the assumption. This similarity is the subject of this chapter. However, before directly dealing with this similarity, it is necessary to make some methodological explanations and introduce a scheme for comparing structures of such a distant nature.
METHODOLOGICAL EXPLANATION
Of course, each scale level has its own unique specificity of natural properties. It is its study that modern science has been engaged in since the Renaissance, and in this it has achieved undoubted success, having accumulated a huge factual material about practically all levels of the Universe organization.
However, much less attention has been paid to phenomena common to all levels. It is natural. After all, to thoroughly study the specifics of each level of the large-scale organization of the Universe, it is necessary to concentrate attention on its inherent features only. If science for 500 years would not reject with unprecedented persistence all attempts of separate thinkers to concentrate attention on general properties of objects, it would hardly reveal all nuances and details of substance structure at each of levels. After all, it was enough to rigidly accept some general scheme of structure, and the study of a large class of phenomena could be stopped there. In this case we would not receive that undoubtedly valuable and gigantic storehouse of information, which at the present stage is already quite "ripe" for generalization at a sufficiently high level of concretization.
Over time, the path of differentiation, for all its necessity, has by now led science into an attitudinal dead end. Having left to philosophy all attempts to find general laws of nature, the Western scientific paradigm for many centuries with a sense of incredulous disdain met any attempts to generalize the laws of different scales. To undertake such work in official science was considered a sign of bad taste, the result of poor education or dilettantism. It was considered impossible to comprehend professionally several disciplines at the same time, and therefore any generalizing theories were met with hostility just because they were generalizing. Meanwhile, this does not contradict the fact that "coryphees in their field" were allowed to write large review works.
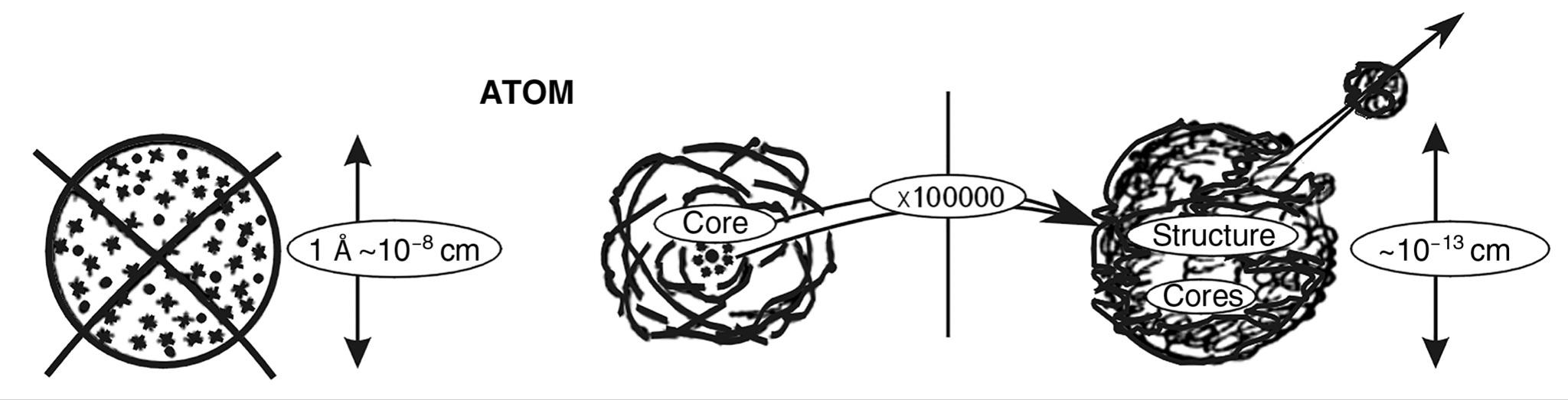Fig. 1.20. The first (polycentric) model of Thompson's atom is shown on the left, which was later rejected and replaced by Rutherford's monocentric model. But the structure of the nucleus was still polycentric (the figure is taken from E. Rogers' book "Physics for the Curious")
At the same time, if these works did not belong to one specific discipline, they often had a purely compilation character, and as a result of such "generalization" there never appeared an emergent effect of integrity. The review did not lead to generalization, from which some supra-subject laws would be born.
This, we repeat, could not have happened without a partial loss of specificity, for the general is always poorer in precision and particularity than its parts. In a tradition where the struggle for ever more precise and detailed knowledge had been going on for centuries, any attempt to propose a theory that would lead to the loss of this precision was certainly unnatural. The maximum that science could do was to use indirect large-scale analogies. The most striking example is the story of the model of the atom.
As is well known, Thompson's model was the first to be proposed, which was a bag of positive and negative charged particles uniformly distributed throughout the volume of the atom (see Fig. 1.20).2
"By 1910, however, this picture was no longer satisfactory. Alpha particles, used as projectiles to investigate the structure of the atom, produced results that could not be explained by the pudding-shaped model of the atom. Rutherford proposed a new model of the atom, almost empty, with a tiny atomic nucleus surrounded by electrons moving in orbits..."3
Here, perhaps for the first time, a S-Analogy was used to solve a global scientific problem, when the structure of the organization of the solar system was fruitfully transferred from the megaworld to the microcosm.
However, the rarity of successful examples indicates that the method of S-Analogies itself did not exist.
Only since the beginning of the twentieth century, the systems approach (A. A. Bogdanov, V. I. Vernadsky) emerged and began to gradually gain weight, within the framework of which a new discipline - THE GENERAL THEORY OF SYSTEMS, or abbreviated "GTS" (L. Bertalanffy, V. N. Sadovsky, Y. A. Urmantsev, etc.) - began to emerge. It was created proactively, by different thinkers in different variants. Each variant practically did not develop the previous one, but appeared as if anew, on an empty place. Each author of "GTS" tried to create anew the whole axiomatics, the whole terminological thesaurus, all the rules. In doing so, he relied on the accumulated knowledge in natural sciences, mainly in sociology and biology, and each author applied his own version of mathematical processing.
Classical physics did not adopt the "GTS". Unification of all large-scale phenomena physicists tried to carry out on the basis of traditional methods. However, everything has to be paid for. Western science paid for accumulation of detailed information by complete loss of integrity of the world picture. And desperate attempts of its best representatives to gather the fragments into a single whole, at least at the most general level of physics - to create a unified field theory, finally failed by the end of the twentieth century, although the prize for the solution of this problem was not serious, at least the Nobel Prize.
In this work we will follow the way of the system approach. The choice of the structural-system method is conditioned by the fact that it is extremely difficult to construct a general physical theory of large-scale regularities "from scratch." It is necessary to approach its solution gradually and step by step. It is necessary to start with the search for the most obvious scale invariants, even at the cost of losing the inherent accuracy of physics. We believe that at the first stages of such a path it is impossible to expect the construction of an exact THEORY OF A UNITED FIELD, which would allow us to combine all specific features of various types of interactions in formulas. It is necessary to define at least the most general invariants, even if expressed in the form of any system schemes and qualitative models. Before we start our way along the S-axis, let us arm ourselves with a simplifying scheme of structural analysis.
Its essence is that all structures are divided into two polemical types: monocentric (M-structures) and polycentric (P-structures).
A typical representative of a monocentric structure is an atom, and a polycentric structure is a chaotic asteroid.
Between them we can introduce a continuous transitive series of intermediate structures, which in our presentation will be called MF-structures.
Without pretending to complete the classification, let us propose an eight-digit scheme, which is formed due to binary combinatorics of three levels of any system: outside - the form, in the depth - the center, between them - the intermediate medium (see Fig. 1.21 below).
Hereafter we will use simplified notations throughout the text: P-structures and M-structures, which are introduced for limit forms (No. 8 and 1), and MF-structures for all intermediate forms (No. 2-7).
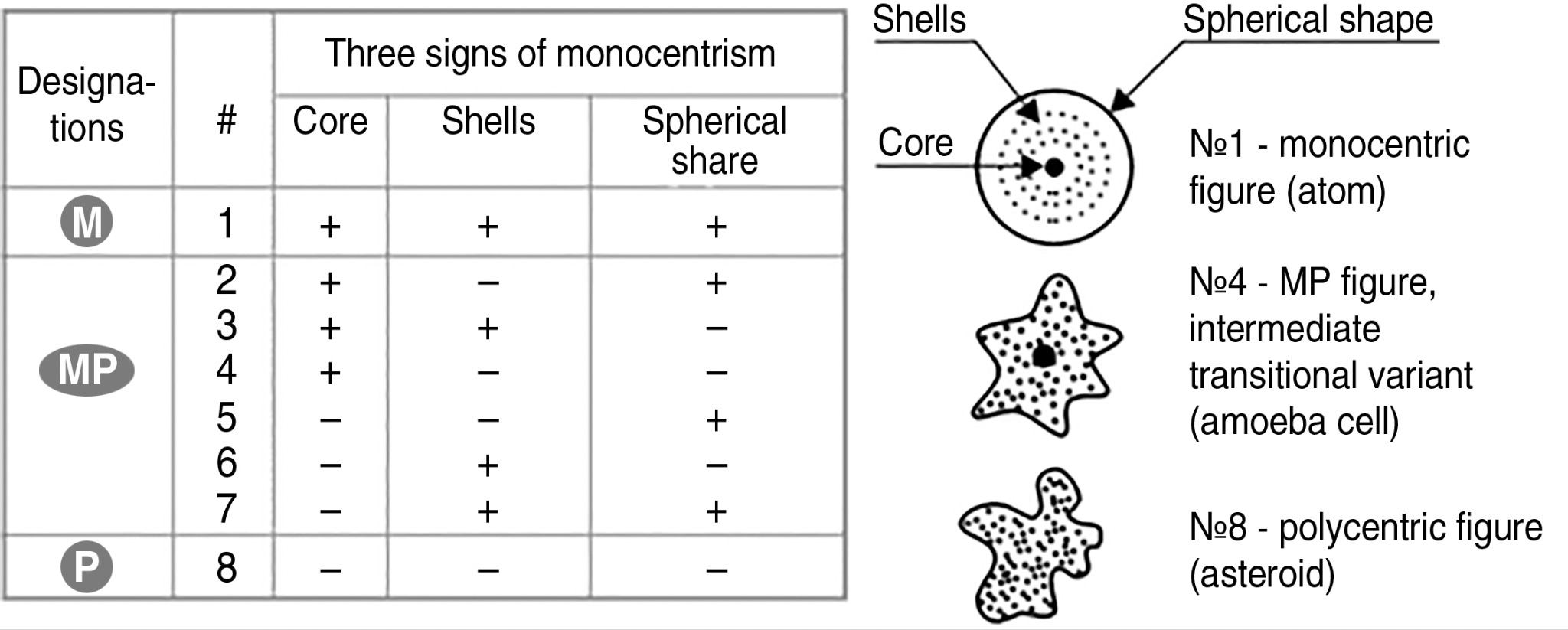Fig. 1.21. Two poles of symmetry of structures and six conditional intermediate types
All three levels may or may not exhibit signs of monocentricity. For the shape, this refers to the presence of sphericity (or near-sphericity, such as ellipticity). For the center, it involves the presence or absence of a central, system-forming core. For the intermediate medium, it pertains to the presence or absence of a shell structure. An additional, fourth, sign of monocentricity has to do with structurization of the external environment around the object - this sign is the presence of radial-radial symmetry for the external shells of the system.
So, returning to the S-axis, we note the following. The preliminary analysis has shown that the macro-interval of the SW, which we have selected, is in many respects similar to the Mega-interval. If it is really so and the whole S-axis is divided between the fields into three equal sections, then it remains to assume that each of these sections has some invariant structural-dynamic properties. Let us check whether it is so.