S-structural invariant
Let us now compare two intervals of 20 orders of magnitude: the MACRO INTERVAL - (II) and the MEGAINTERVAL - (I) (cf. Fig. 1.26 and Fig. 1.35).
Immediately striking is their amazing, though not absolute CONNECTION with a COEFFICIENT of \(10^{20}\).
Let's review it step-by-step:
-
Both intervals are bordered on the left by polycentric structures:
II - internal parton structure of nucleons (< \(10^{-13}\) cm);
I. - Chaotic shape and coreless structure of asteroids (< \(10^7\) cm).
-
The beginning of the first order is marked by the appearance of the first sign of monocentrism - spherical shape:
II. - protons and neutrons;
I - spherical minor planets (like Mimas) and NS.
-
The first order is dominated by monocentrism of the form:
II - nuclei of atoms;
I - minor planets.
-
At the first order, the structure moves from micropolycentricity to macropolycentricity (the constituent elements become of the same order as the system):
II - nucleons in the nuclei of atoms;
I. - mascons inside planets like the Moon, hypothetical nuclei in the cores of stars.
-
On the first order of the two intervals are remarkably similar (in terms of element composition and packing) systems:
II. - atomic nuclei are made up of nucleons;
I. - neutron stars are made up of nucleons.
-
From the first to the fifth order, the dominance of monocentric structures increases, purely polycentric systems are practically absent, the first wave rises of both intervals are "populated":
II. - with atoms;
I. - planets, stars.
The exception is first orders, which combine external monocentrism with internal polycentrism:
II. - the nucleonic structure of nuclei;
I. - The mascon structure of the minor planets.
-
From the fourth to the fifth order, both intervals are populated exclusively by monocentric structures with three distinct features:
II. - mesoatoms, positive ions, i.e. atoms with electron shells "stripped" to different degrees;
I - Earth- and Jupiter-type planets, single main-sequence stars.
-
At the fifth order of intervals, fully monocentric structures are finally formed, possessing three functionally important features: a nucleus, spherical shape, and shell structure (with points of average size surprisingly equally spaced on the S-axis, but with a step of 20 orders of magnitude)
II - average sizes of atoms;
I - average sizes of stars.
-
From the sixth order, the elements begin to form systems of the first kind:
II - molecules and crystals;
I. - paired stars and star clusters.
-
From the crest of the first waves and practically to the end of both intervals, polycentric structures dominate for 15 orders of magnitude: II. - molecular environments, crystalline (amorphous) structures; I. - stellar systems of all kinds, to super clusters of galaxies made up of stars.
-
At the eleventh order of intervals, exactly between the two waves, the monocentricity of the structures is revived in the S - Trough of Potential stability (STPS) in an incomplete way: II. - balls of cosmic (volcanic) dust, cells; I - galactic nuclei, quasars, planetary nebulae.
-
On the eleventh order, monocentrism is partially manifested: spherical shape, nucleus and shells may occur separately.
-
Monocentrism rarely, at the level of statistical background, occurs up to order 15 as a spherical shape or a shape with radial symmetry: II - bird and animal eggs, seeds and flowers of plants on the Macro interval; I - globular star clusters and elliptical galaxies on the Megainterval.
-
At the fifteenth order of intervals some system convolution is formed, which leads to the formation of polycentric systems of the second kind with a new level of elemental base: II - on the Macro-interval at the transition from the 15th to the 16th order is the median of the size distribution of vertebrates, which later begin to create their own systems: families, flocks, herds, social systems; I. - The 15th-16th order of the Mega Interval - here passes the median of the size distribution of galaxies, which further "begin to create" pairs and nests, clusters and superclusters.
-
Both intervals end in exclusively polycentric structures: II. - asteroids, biocenoses and societies; I - super clusters of galaxies forming the filaments of the cellular structure of the Metagalaxy.
Thus, we see that the similarity of the two intervals is manifested practically along their entire length. All this allows us to identify a certain STRUCTURAL INVARIANT, 20 orders of magnitude long, which as if twice unfolds on the S-axis, "starting" from the sizes \(10^{-13}\) cm and \(10^7\) cm, i.e. exactly after 20 orders of magnitude (see Fig. 1.43).
Of course, since the Macro and Mega Intervals are located in different places of the scale ladder of the Universe, one can find a structural difference between them besides structural similarity.
Let us consider this STRUCTURAL DIFFERENCE step by step.
- The presence of "meganucleons" in the structure of stellar nuclei has not yet been revealed by astrophysics. If it is absent, it leads to a strong structural difference between atomic nuclei and stellar nuclei.
- There are no nuclei of atoms whose sizes are beyond the first order of the Macro interval.
At the same time, for the Mega-interval, the astrophysical theory gives values of the sizes of stellar nuclei up to at least the third order inclusive. It is possible that either the astrophysical model of stellar nuclei is not correct here, or there are rare atomic nuclei with sizes 1000 times larger than nucleons, which have not yet been discovered on the Macro-interval.
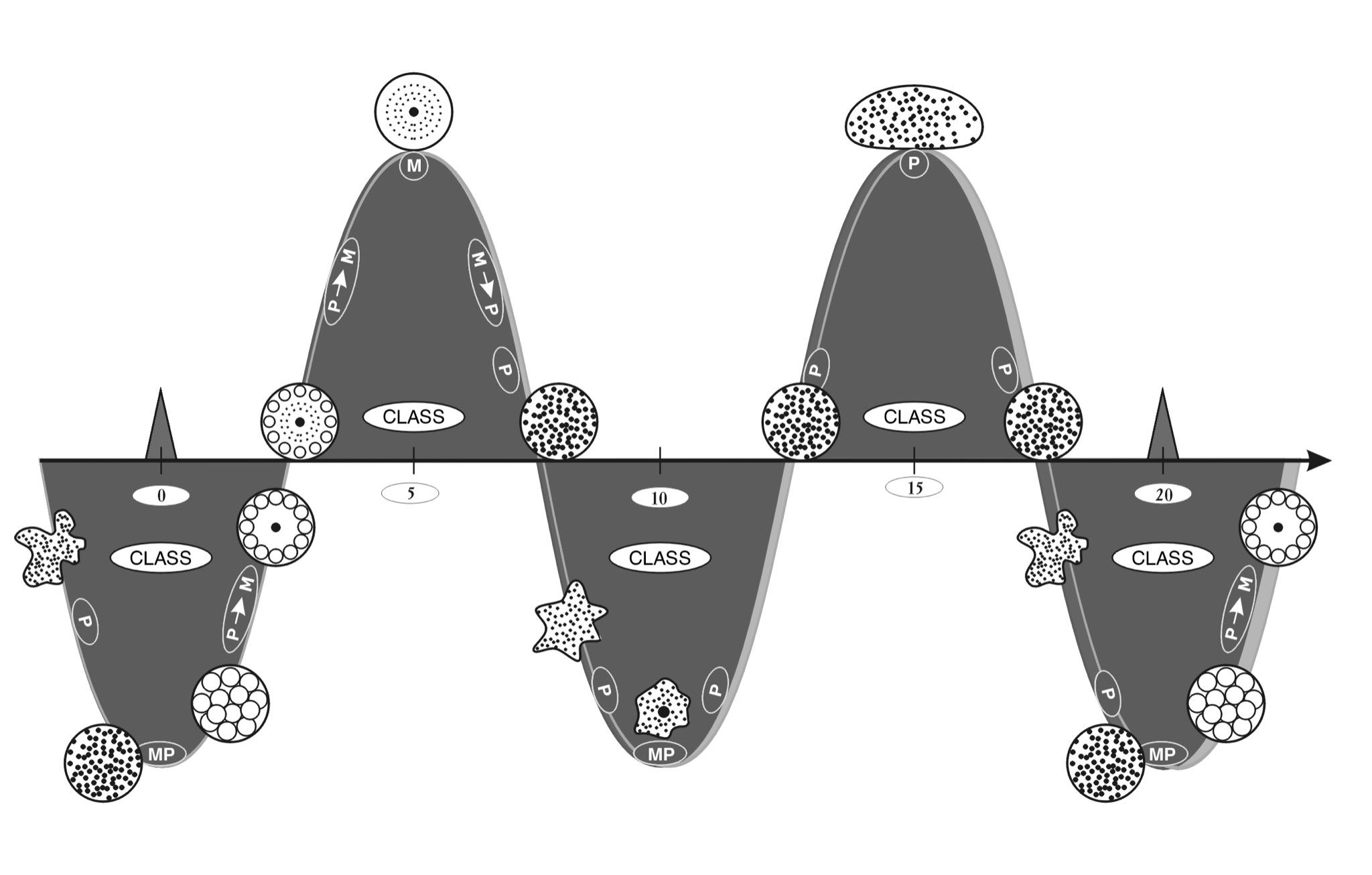 Fig. 1.43. S-Structural invariant
Fig. 1.43. S-Structural invariant
- Stars are known whose sizes are two orders of magnitude larger than the average stellar size; these giants occupy the seventh and eighth orders of the Mega Interval, forming the fully monostructured upper part of the first wave.
At the same time, the author has not encountered in the literature any mention of atoms with sizes exceeding ten angstroms, hence, the seventh and eighth orders of the Macro-interval are not "populated" with atoms. This difference, however, may not be so significant, if we take into account that such giants of the Mega-interval, which would have diameters greater than \(10^{13}\) cm, are very few among the stars, and they are not mentioned in the literature. Astronomers know them only because of their high brightness.
Besides, examples of centrosymmetric clusters of atoms are known on the macro-interval. The sizes of these clusters fall just on the seventh order, and at the same time they sufficiently realize the monocentricity of the structure.
-
Most stars have sizes of the fourth and fifth orders of magnitude of their interval - these are dwarf stars. Dwarf stars outnumber other stars in the Universe. Most atoms (hydrogen), on the other hand, have sizes of the sixth order of magnitude.
-
Polycentric systems of atoms - molecules - are made up of elements that are very close together, at distances commensurate with the size of the atoms themselves. The distances between stars in "stellar molecules" - paired and multiple systems - are often many times larger than the stars themselves. Therefore, "stellar molecules" unlike ordinary molecules are extremely rarefied systems.
-
The second ridge of the Megainterval on its rise is represented by a set of systems with near spherical (elliptical) symmetry - elliptical galaxies.
We do not observe anything similar on the rise of the second crest of the Macro-interval. Perhaps, at the first stages of the Biosphere evolution, these scale sizes could have been massively represented by protozoan colonies, which, as is known, often take a sphere-like shape.
The point is that the evolutionary age of galaxies is much less than the evolutionary age of the Biosphere, if it is measured not by the number of years, but by the number of birth cycles. In this sense, many galaxies are just babies that first appeared in the Universe, whereas biosystems have undergone a very long and complex path of evolution. Therefore, it is more correct to compare the Mega-interval with the primary biosystems of the Macro-interval, i.e. in this case with the first cells and the first colonies of them.
So, it is quite natural that the MACRO INTERVAL has, besides similarities, many differences from the MEGAINTERVAL. It is very likely that these many differences are connected with the fact that our ideas about macro-structures were formed in very specific and unique conditions on the surface of the Earth, and we cannot even imagine how the Macro-interval is organized on other planets, not to mention other galaxies. At the same time, we have an opportunity to judge the structures of the Mega-interval more objectively, because we observe the cosmos from the side and collect average statistical information about it.