MEGA-Interval

Let us consider the Mega-interval (Fig. 1.34). It starts from the right border of the Macro-interval - with the sizes from \(10^{7}\) to \(10^{8}\) cm.

In this size range, two types of systems are of particular interest: planets and stellar cores. On the Earth, structures of this scale are fragments of the lithosphere, the study of the regularities of their size distribution87 has only recently begun. PLANETS (CLASS #8). Up to the size of planets, cosmic bodies are not monocentric. All cosmic bodies in the range from atomic size to asteroids have polycentric structure - they are composed of atoms uniformly or chaotically distributed throughout their volume. The reason is the short-range action of electromagnetic forces at such scales. There is no smoothing of shape: all bodies have a pronounced chaotic, fragmentary shape.

As was shown in Chapter 1.3 (see Fig. 1.10), the real boundary between formless asteroidal bodies and spherical planetary forms is somewhere in the neighborhood of 300-500 km. Thus, in the range from \(10^{7}\) to \(10^{8}\) cm, both polycentric and monocentric bodies are found, with a tendency to transition from polycentrism to monocentrism as the size increases. It is very important to note that a similar situation with the structural transition can be found on the S-axis, if we move along it exactly 20 orders of magnitude to the left. We have shown above that it is there that the transition from polycentrism to monocentrism takes place in atomic nuclei.

Thus, it is from the first order of the Megainterval that the spherical bodies of planets begin to form. Let us consider when other signs of monocentrism appear: nuclei and shell structure.

There is no reliable evidence that planets smaller than 1000 km (\(10^{8}\) cm) have nuclei. Perhaps the Moon, which is \({3.4}\cdot{10^{8}}\) centimeters in diameter, has a nucleus. "According to the velocity distribution ... the Moon may have a small core with a radius of a few hundred kilometers. The core is in a molten or semi-molten state, since transverse waves do not pass through it, and consists of Fe-FeS solution."1

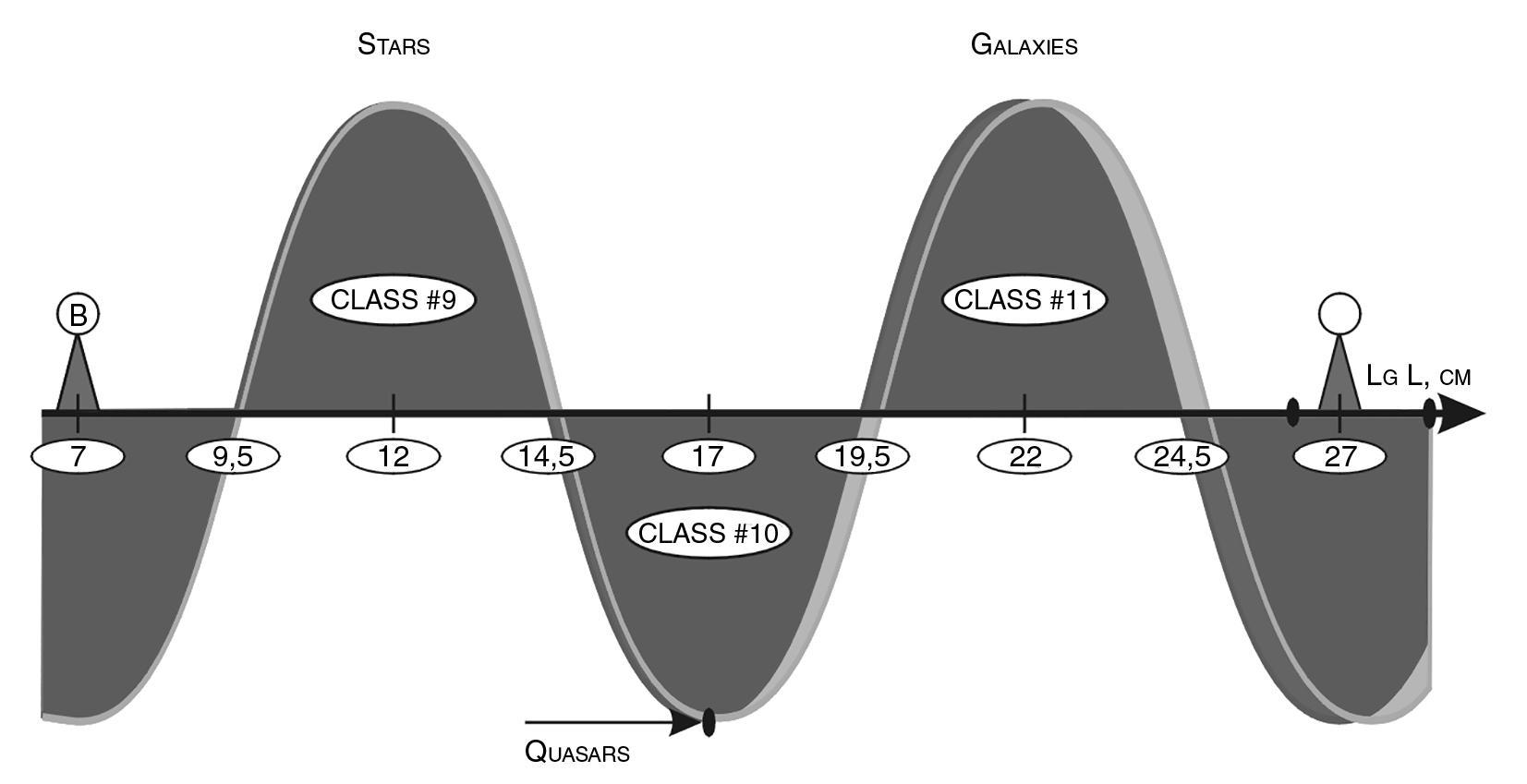Fig. 1.34. A mega-interval of 20 orders of magnitude extends from point B to point C

Since the magnetic field is an indirect sign of the activity of the planet's core, a sign of its presence, then by its magnitude you can tell if a planet has a nucleus. Thus, the Moon has a magnetic dipole \(10^{6}\) times smaller than that of the Earth and 300 times smaller than that of Mars. However, even Mercury, which has a diameter of 5000 km, has a magnetic field of about 0.7% of the strength of the Earth's magnetic field2, which allows planetologists to assume that it has an iron core occupying 50% of the planet's volume. As for the Earth, whose dimensions exceed \(10^{9}\) cm, there is little doubt that it has a core — it has an inner core3 with a diameter of more than 2000 km (\(~10^{8}\) cm).

The spherical Moon, which probably has no pronounced core, most likely has a polycentric internal structure. The fact is that strong gravitational inhomogeneities have been found on its visible side4. "In 1968, Muller and Sjögren, studying the gravitational field of the Moon, discovered large positive anomalies and introduced the concept of mascons as sources of these anomalies"5. Subsequently, "when the first spacecraft launched into orbit of the satellite of the Moon began their work, scientists were surprised to find that the satellite of the Moon moves somewhat unusually. In its movement were noticeable small jerks ... It turned out that the outer layers of the Moon to a depth of several hundred kilometers is not homogeneous. It is as if a number of large blocks, sprinkled outside sand (italics mine — S. S.), giving the whole structure the shape of a ball. Some of the mascons even go to the surface of the planet."6 This suggests that there are large formations in the body of the Moon, which were either embedded in it after its formation, or formed as a result of internal processes, or are the remains of large primary bodies. Their mass is of the order of \(10^{21}\) grams, which allows us to estimate the order of magnitude of these large formations at about \(10^{7}\) cm. This fact shows that for such planets as the Moon (and the Earth), primary bodies of hundreds of kilometers in size could be components that entered the planet as independent ready-made blocks. This leads us to the simple conclusion that small planets in the 100–1000 km range may have a blocky-polycentric rather than shell-like structure. Hence, planets, like the nuclei of atoms, may have a mixed MP structure. The PROPOSAL of a heterogeneous structure of small planets is consistent with the jet stream model of H. Alven and G. Arrhenius7. It is unlikely that only one primary nucleus was formed from the primary cosmic dust in the jet stream, on which the dust would then adhere (such a mononuclear model can be called the "snowball" model). Calculations of the rate of sticking of particles on one planetesimal nucleus, as estimated by these authors, showed that such a process could not have led to the formation of planets even during the entire existence of the Solar System. Most likely, several such clumps were formed in parallel, and only then their macro assembly occurred (such a model of planet formation can be called the "snowball" model). At the moment of final assembly of the planet from giant blocks, a part of planetesimals due to powerful collision impacts collapsed, forming meteorites and asteroids. Estimating the size of planetesimals provides a boundary that has a special place in SWS: "On the basis of interpretation of the available data on the peculiarities of crystal growth in iron meteorites in the presence of diffusion, the sizes of bodies appear to be of the order of a hundred or several hundred kilometers"8.

Thus, there are many reasons to believe that polycentricity with a scale of inhomogeneities of 100-1000 km is the result of the macro assembly of planets at the final stage of their appearance. Traces of it, apparently, are preserved in larger planets of the Earth group, although their manifestation here is distorted by gravitational forces.

So, it can be PROPOSED that from a size of \(10^{7}\) cm to a size of \(10^{9.5}\) cm (i.e., for all Earth-group planets and minor planets), the heterogeneity of structure should play a much larger role than in modern theories of planetary structures based on traditional shell models. (Of course, for these planets, the shell structure also plays a huge role, which, together with the block structure, organizes the complex structure of planets of the Earth type.) Here it is also important to note that the scale of the main planetary blocks, as estimated by various authors, converges on sizes of hundreds of kilometers, which exactly corresponds to the lower region of the nuclear half-wave of the Mega Interval: \(10^{7}-10^{8}\) cm.

On the basis of the above we can draw a very important CONCLUSION. At the \(10^{7}-10^{8}\) cm boundary there is a change of the POLYCENTRIC STRUCTURE of cosmic bodies to MONOCENTRIC.

And while for small planets the question of the presence of a core and a clear stratification by density into deep bodies is debatable, for terrestrial scale planets (greater than \(10^{9}\) cm) this question does not arise.

Already for Mercury (\(5 \times 10^{8}\) cm) the presence of the nucleus is not doubtful. Consequently, if the first sign of monocentricity — spherical shape — appears somewhere at the boundary of sizes \(3 \times 10^{7}\) cm, then the second and third signs — nucleus and shells — appear, apparently, somewhere at the boundary of \(3 \times 10^{8}\) cm (see Fig. 1.35).

STAR NUCLEI (CLASS NO. 8). "Living" stars have sizes larger than \(10^{10}\) cm, so there are no representatives among them that would be located on the S-axis in the scale zone of the transition from polycentrism to monocentrism (\(10^{7}-10^{8}\) cm). But it is in this size range that neutron stars (NS) are located. What are they?

According to R. Wald, the NSs are huge nuclei similar to atomic nuclei. Indeed, like nuclei, they consist exclusively of densely packed nucleons (all electron shells of former atoms are destroyed by gravity). Because of this, the NSs have a monstrous density, the same as the nuclei of atoms.

So, neutron stars are polycentric systems — in many respects similar in structure to the nuclei of atoms. Isn't it amazing that nature has placed these exotic objects in a size range that is almost exactly \(10^{20}\) times the size of nuclei!? What could be a better example of the scale similarity of structures at such gigantic scale distances!? Let's turn to the MACRO INTERVAL for a moment. From the left and right edges of the Macro-interval Nature has arranged the nuclear type of structure. Moving along the S-axis from left to right, one can see how at "entering" this interval the P-structures of the Micro-interval are transformed into the M-structures of the Macro-interval (see Fig. 1.26), and similarly at "leaving" it: the P-structures of the Macro-interval are transformed into the M-structures of the Mega-interval. WHAT IS AT THE TOP IS ALSO AT THE BOTTOM.

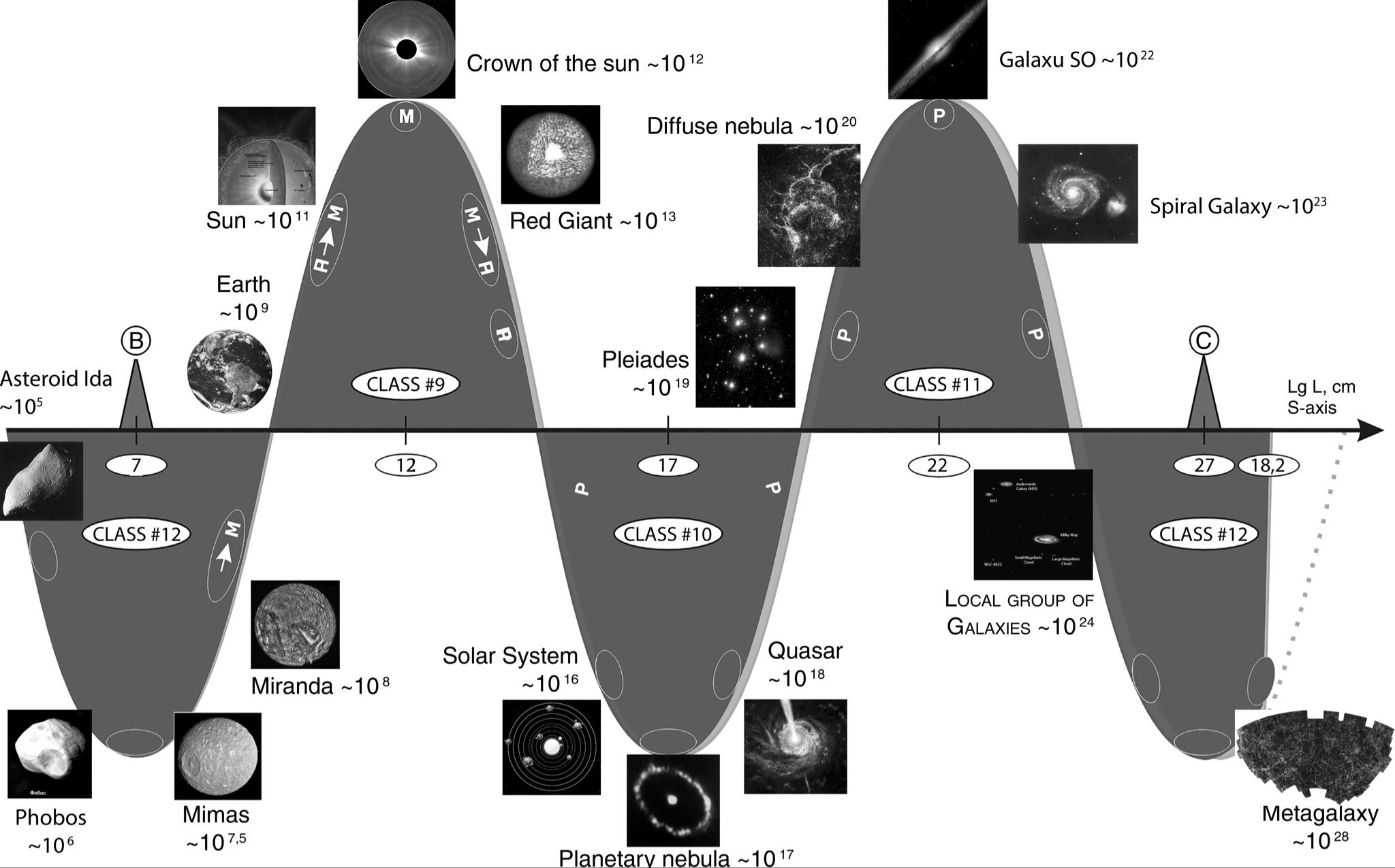Fig. 1.35. Mega-interval showing the transition from polycentrism to monocentrism. Dimensions are given in cm

However, besides similarity, there is also a difference (however, probably imaginary). Thus, atomic nuclei consist of nucleons, the number of which does not exceed a few hundreds, while the NSs consist of a huge number of nucleons — of the order of \(10^{60}\). Obviously, within the framework of the classical approach, there is not and cannot be complete structural similarity here. For a full structural similarity neutron stars (NS) lack a macro cluster structure. However, such a structure cannot appear due to electromagnetic forces, because on such scales they simply cannot compete with gravitation in their effect on matter. And even more macro cluster structure cannot be a consequence of gravitational forces, which have a strict central symmetry. In spite of this, can we still hope that nature has taken care of the full scale similarity with a step size of \(10^{20}\)? If so, then the sizes of the order of \(10^7\)-\(10^8\) cm should be characterized by structures that are not just polycentric, but cluster-polycentric. In other words, EOs should consist of dozens of or hundreds of mega clusters.

However, in astrophysical theory, in principle, there is no place for the mega cluster model of NS. In most theoretical models, neutron stars have a partially shell structure 9 (see Fig. 1.36). It is impossible to imagine any other structure based on the classical idea of gravitational and electromagnetic forces of nature. After all, gravity is the dominant force for EOs (because of their monstrous density and mass). It can only pull the matter to the center of mass. At that, if any diversity is possible, it is only due to segregation of matter by density in strict dependence on the distance to the center of mass. That is why in classical astrophysics it is impossible, even by way of hypothesis, to assume the existence of a globally polycentric structure in such objects as the EO.

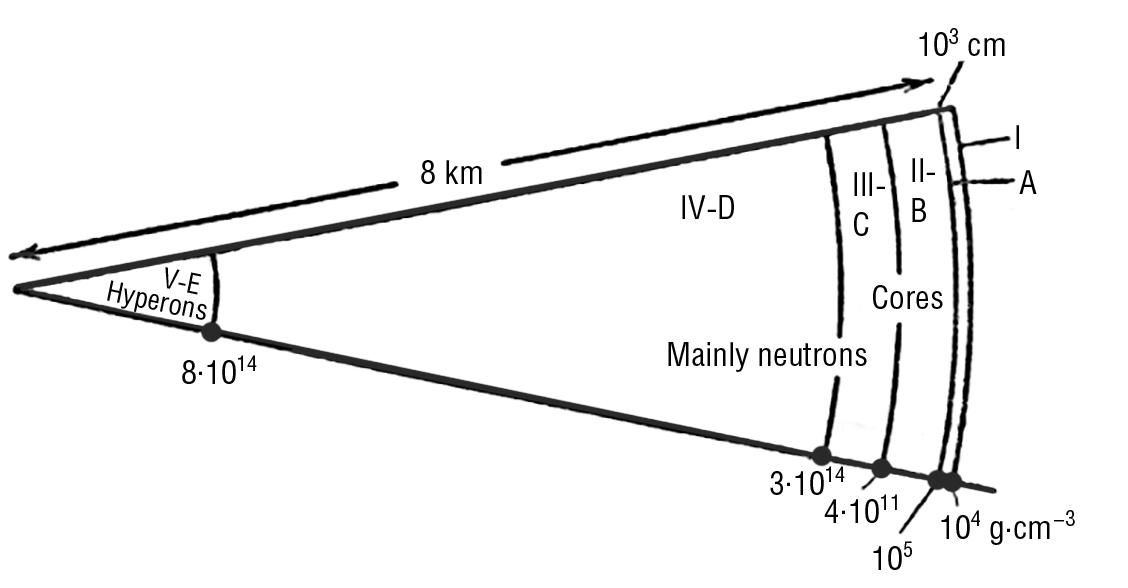
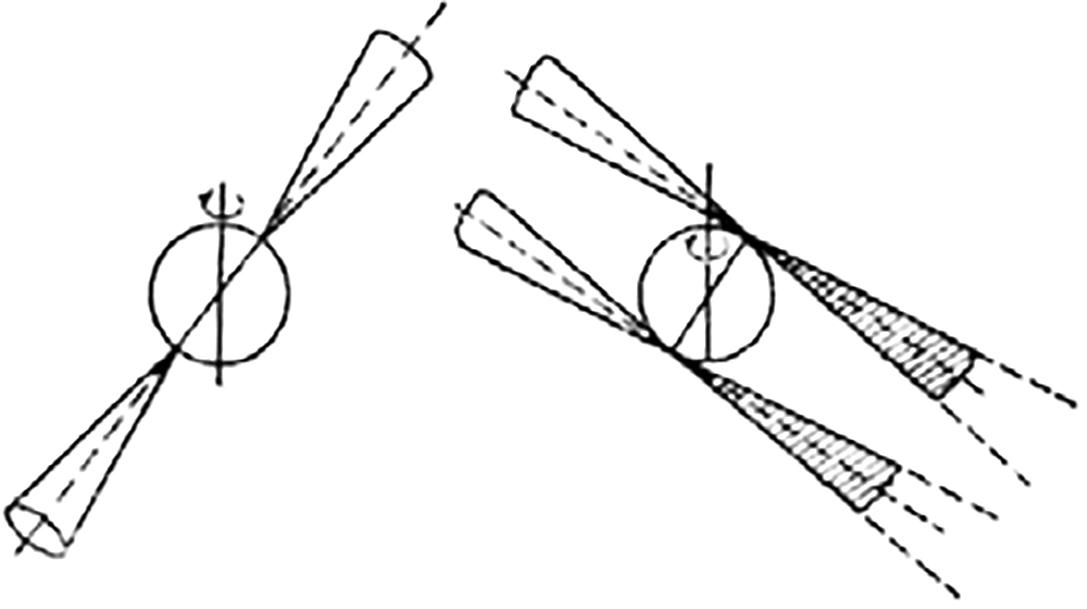Fig. 1.36. А. Probable block-polycentric structure of a neutron star (in the author's opinion). B. The shell structure of a neutron star (according to I.S. Shklovsky). C. Fan model of pulsar emission (according to I.S.Shklovsky)

There is absolutely no theoretical basis in the theory of gravitation for the appearance of any "mascons" or "separateness" within objects such as EO.

However, observations of the EO have brought so many paradoxical puzzles that the shell model, in fact, does not withstand any criticism today. Let's consider these riddles and in general the PROBLEM of stars' cores in details.

Astrophysics knows little about the structure of the nuclei of stars and other formations of such small sizes. In all cases, this is the domain of modeling. The exceptions are neutron stars and white dwarfs - naked nuclei, which are accessible to direct observation. However, because of their great remoteness and small size, their structure also remains the domain of theoretical calculations based on indirect data on mass, luminosity, etc. parameters. Nevertheless, those neutron stars that are in an active state provide additional information about themselves. We are talking about pulsars.

Pulsars were discovered in the 1960s and since then have never ceased to amaze and baffle astrophysicists. It turned out that pulsars are neutron stars rotating at tremendous speed and emitting short pulses of radio emission. Since neutron stars are formed from rotating stars of much larger size, based on the condition of conservation of momentum, the equatorial velocity of a contracting star must increase by as many times as its radius decreases (think of the rotation of a figure skater on ice). "At the final stage of contraction, when a neutron star is formed, its equatorial velocity can be enormous, even close to the speed of light!" 10 If the Sun suddenly became a neutron star, its rotation period would be reduced from 27 days to one ten-thousandth of a second.

Imagine now that in open space in vacuum a sphere with a giant (nuclear) density rotates at a tremendous speed, since it consists of almost only nucleons. The size of this sphere is about 100 km. Such a giant wolf has no reason to slow down, because it rotates in the void; there is no reason to lose energy, because all nuclear reactions in it have already stopped; there is no reason to change its size by leaps, because according to the accepted theoretical models it is a homogeneous body; there is no reason to have inhomogeneities on the surface, because gravity, which created and holds it, gives it strictly spherical symmetry and does not allow any deviations from it.

Contrary to all these obvious reasons for astrophysics reasoning, pulsars violate them and violate them so clearly that they leave no chance to ignore their paradoxes.

"...There are more than enough unsolved problems in the physics of neutron stars... It must be said bluntly that to date there is no universally recognized quantitative theory... of pulsars." 11

The first task of pulsar physics is "to understand why rotating neutron stars brake, thus continuously releasing energy." 12 As I.S. Shklovsky's analysis of this question showed, magnetic fields cannot cause this effect. The most probable cause, according to I.S. Shklovsky, is the emission of gravitational waves by the pulsar, but what it is — classical physics still cannot determine. The second task is to explain the phenomenon of "star-shaking" — a jump-like decrease in the rotation period of the pulsar. "Such a strange phenomenon can only be explained by a real jump-like change in the rotation period of a neutron star. The change in the rotation period, in turn, must be a consequence of a sudden decrease in the moment of inertia of the star, caused by some complex processes in its interior." 13

The third task is to explain the "fan" or "pencil" character of pulsar radio emission. The point is that a pulsar shines like a lighthouse — a narrow rotating beam, which we see only at the moment when it "brushes" the Earth with it (see Fig. 1.36B). At the same time, pulsar emission profiles consist of much narrower sub-pulses.

According to I.S. Shklovsky, such a phenomenon can be caused only by the "spotty" structure of the radiating surface of pulsars. Moreover, each spot is strictly fixed relative to the pulsar body and does not wander around it, neither disappears nor appears unexpectedly. Thus, this "panther coloring" of the pulsar can serve as its radio passport.

"What reason 'keeps' the radiating spots in strictly defined regions around the rotating star?" — asks I.S. Shklovsky. He answers that "such a reason can only be a very strong magnetic field." 14 Although he does not explain how an absolutely homogeneous ball filled with neutrons (hence the name of stars) can have such a rigidly inhomogeneous magnetic field. His reasoning, however, can be understood.

Gravitational forces are initially monocentric and are not able to create heterogeneity at such masses and sizes, so it remains to attribute everything to magnetic fields, in classical astrophysics there is simply no other option. In this case, the calculations should give convergence. What is there to check?

Of course, astrophysicists are somehow trying to explain all these bright anomalies, but all attempts to build models of pulsars remain unsuccessful. The reason for this, in our opinion, is the failure to take into account the peculiarities of the location of pulsars on the S-axis.

After all, if the scale similarity with the coefficient \(10^{20}\) is real, then pulsars should be similar to the internal structure of atomic nuclei, i.e., have a macro-polycentric structure. Their nuclei should be as inhomogeneous as the nuclei of small planets of the same size range. And these "mascons", or inhomogeneities, of neutron stars can create a gravitational imbalance of the star's body, which will cause it to lose energy (gravitational waves). These same inhomogeneities, in the author's opinion, are the cause of the "spotty" radiation of the pulsar.

Finally, since the process of compression of the EO continues, from time to time the macroclusters move relative to each other, which can occur as a jump due to the commensurability of their sizes with the body of the star itself. Hence the "starquakes". Such shaking of macroclusters leads to a gradual decrease of the radius of the star and an increase in its rotation rate.

If we now compare two models of the internal structure of pulsars - the traditional, monocentric one, based on the theory of classical gravitation, and the scale-like one, taking into account the laws of scale similarity of the Universe (see Fig. 1.36), it turns out that in the second model all the riddles have one cardinal solution - megapolycentricity! Thus, the MS-invariant model with a length of 20 orders of magnitude predicts that Pulsars should have a POLYCENTRIC STRUCTURE, contrary to all traditional theories. What is the mechanism of formation of such MACROCLASTERS?

After all, none of the known forces of nature can lead to their appearance. Let us put forward a preliminary HYPOTHESIS.

In the area of 100-1000 km in size there is an unknown to science Fifth Force - the antipode (or analog) of the strong interaction. It is responsible for the formation of different size separations, and first of all - for the formation of separations with sizes of 160 and 500 km.

This force forms the megacluster structure of small planets, neutron stars, and inner cores of stars. It is this fifth force that creates inhomogeneities inside pulsars, which lead to the above phenomena.

The hypothesis has one essential problem. It unambiguously follows that the star cores should have quantized mass because of the megacluster structure of the order of 100-1000 km. The data in favor of their supposed heterogeneity the author has not found yet. If this heterogeneity really exists, it will be possible to detect it by the following indirect manifestations.

First, the statistics of the mass spectrum of stars as well as of atoms should in this case have a quantized (polymodal character).

Secondly, many processes inside stars should have quantized discrete character normalized by some conditional minimal mass unit, which will be unified for all stars. This conditional unit is an analog of the nucleon in the atomic nucleus. We cannot say anything about its mass, but it should have a size close to 160 km (or another option - 500 km, its origin will be discussed further on).

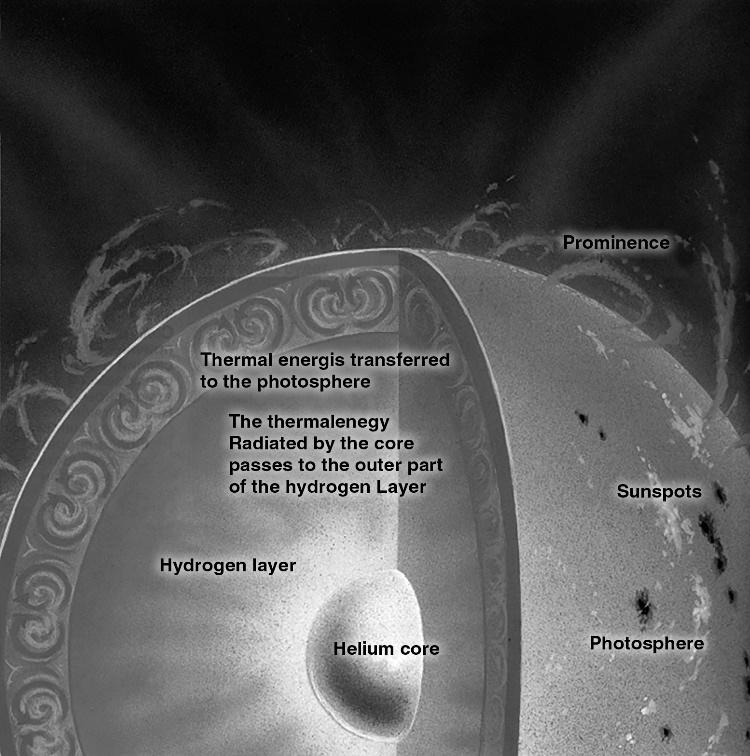Fig. 1.37. Structure of the Sun, which is a typical star

Thirdly, the Sun cannot be an exception to the rule, so if our assumption about megaclustering of stellar nuclei is correct, there could well be moments in the life of the Sun when quantum, jump-like changes of global scales occurred in it. Obviously, their traces should remain on the surface of planets, which can be checked on the Earth and Moon, analyzing the features of ancient sediments.

Using the similarity of the two intervals Macro- and Mega-, we can remember how the analogy with the planetary system helped to reveal the structure of the atom and its nucleus. Now it is time for the microcosm to pay its debts - to tell us how planets and stars are organized. And if the established structural-scale invariants are really real, then in the future their use can help to solve a huge number of problems of scientific knowledge of the world. After all, the regularities of those parts of the S-axis, which are well known in the megaworld, can be transferred to the macroworld, and vice versa. And it is possible to construct the whole left Micro-interval using regularities of Macro- and Mega-intervals. It is only necessary to remember that in addition to scale similarity there is also scale "goodness," or individuality, inherent in each interval separately. STARS (CLASS #9). Let us consider the Mega-interval further.

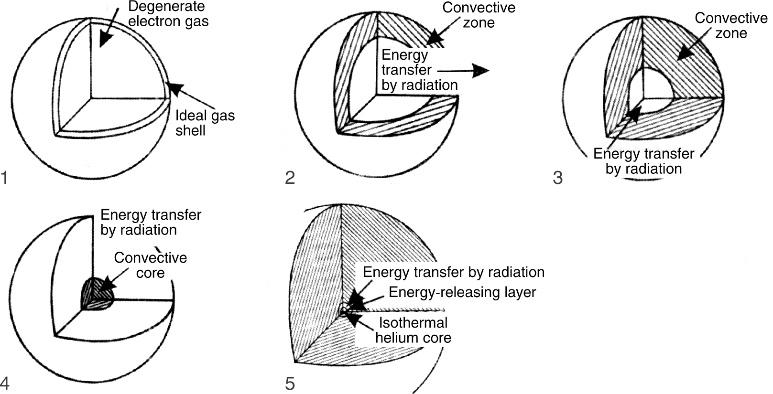Fig. 1.38. Models of the internal structure of stars (according to I.S. Shklovsky) depending on the sizes

Stars are located to the right of the EO and planets on the S-axis. Stars are typical M-structures with all three features: they are spherical, they have nuclei, and their structure is shell-like (see Fig. 1.37). It is noteworthy that with the transition from small-diameter stars to increasingly large stars, the growth of nuclei15 lags behind.

Thus, while the Sun has a core size of 1/4 of its diameter, the red giant has a core size of only 0.001. Consequently, the larger the diameter of the star, the smaller the ratio r / R, where R is the radius of the star and r is the radius of the core (see Fig. 1.38).

This information is important for the HU model. It implies that there is a certain size threshold for stellar nuclei, over which they do not pass. The analysis of stellar models shows that, most likely, this threshold is equal to \(10^{10}\) cm. In particular, "in the center of a red giant there is a white dwarf" 16.

At the same time, as is known 17, white dwarfs have sizes from \(10^{8}\) to \(10^{10}\) cm. Therefore, as we move along the S-axis from the half-wave of stellar nuclei (CLASS No. 8), we get to the stellar half-wave (CLASS No. 9), "leaving" the nuclei beyond the threshold of the crossing of the SW with the S-axis. While white dwarfs (WDs) are homogeneous spheres with neither core nor shells, the middle star of the main sequence (MS) already has both a core and a spherical shape, while in the model of a red giant (KG) the core remains small — (WD). Let us repeat that the sizes of the nuclei of stars do not exceed \(10^{10}\) cm, i.e., they do not exceed the nuclear class threshold. Since the stars themselves can reach gigantic sizes — up to \(10^{14.5}\) cm, the ratio between them and their nuclei exceeds 1000 and can theoretically reach the proportion of \(10^{5}\). Recall that this is the proportion between atoms and their nuclei!

Stars are the most symmetric systems of the Universe. Their spherical symmetry is an example of an ideal M-type shape. There is no reason to doubt that the internal structure of stars has a shell character. At the same time, according to the modern theory of stellar thermonuclear synthesis, it is the core of stars that is the main source of its thermal energy.

Thus, stars exhibit the full set of characteristics of monocentric systems: a central core that is vital to the entire system, a shell structure, a spherical shape, and a radial-beam corona surrounding the star (see Fig. 1.39).

It remains only to establish whether the nuclei of stars are as tiny in relation to the size of the stars themselves as the nuclei of atoms are in relation to the atoms themselves. This may well be expected, based on the scale similarity between stars and atoms, which are exactly 20 orders of magnitude apart on the S-axis.

If this assumption is confirmed by further investigations of the internal structures of stars, it will be another amazing example of perfect scale similarity. If the proportion \(10^{5}\) is not found for stars, it will mean that the scale similarity is partially broken in nature on this section of the S-axis, which must have its own reasons. So far, only the following CONCLUSION is certain: the average size of stars is exactly \(10^{20}\) times the size of the hydrogen atom.

So, returning to the beginning of the MEGAINTERVAL, we find the same abrupt transition from polycentric to monocentric systems as at the beginning of the MACRO INTERVAL. Fig. 1.39. Different shapes of the solar corona. On the left are the coronal shapes during the solar minimum, on the right — during the solar maximum. Radial-radial symmetry can be seen.

P-structures, which prevail before the beginning of these intervals, are quickly replaced by pronounced MF-structures, which finally transform into M-structures exactly after 5 orders of magnitude from the initial points of the intervals (see Fig. 1.35).

Similarly to the MACRO INTERVAL on the MEGAINTERVAL, we see that the change from P-structures (via transient MS-Dorms) to M-structures occurs in the interval of the first five orders (from \(10^{7}\) to \(10^{12}\) cm), with M-structures completely dominating in the size interval from \(10^{9}\) to \(10^{12}\) cm, i.e., on the rise of the first hump of the MEGAINTERVAL. However, since there are giant stars that reach sizes of \(10^{14.5}\) cm, when assessing the prevalence of fully monocentric structures in the MEGAINTERVAL, it should be noted that, in contrast to the situation in the MACRO INTERVAL, they occupy the entire upper hump of the SW (stellar class CLASS No. 9), i.e., 5 orders of magnitude. We note once again that the left part of this hump with a length of 2.5 orders is "populated" exclusively by M-structures. There is no information about the existence in nature of P-structures with sizes from \(10^{9.5}\) to \(10^{12}\) cm!

New types of structures appear on the S-axis beyond the top of the stellar ridge. Pair stars and systems of stars (Classes No. 9, 10) are a kind of stellar "molecules." Is it not surprising that their appearance on the S-axis is exactly 20 orders of magnitude away from the similar appearance of molecules made of atoms on the MACRO- INTERVAL? Let us consider in more detail the location of stellar systems on the S-axis.

The path to the right along the S-axis from the \(10^{12}\) cm crest leads us first to paired stars, then to multiple systems, to groups, and ends in the region of globular and scattered clusters (up to \(10^{20}\) cm in size)18. All these stellar systems are polycentric. The globular clusters, whose diameters occupy the range \(10^{19}\)-\(10^{20}\) cm, are somewhat of an exception (this is an echo of monocentrism, as is the case everywhere at the points where the SW intersects the S-axis). The distances between all paired stars lie in the range19 of \(10^{11.5}\) to \(10^{17.5}\) cm. Consequently, all the paired stars inhabit exclusively the right slope of the first ridge of the MEGAINTERVAL.

All STAR COLLECTIONS - scattered and globular - are located in a rather narrow size range20 - from \(6 \times 10^{18}\) cm to \(10^{20}\) cm.

Consequently, astronomy is not yet aware of polycentric structures with sizes ranging from \(10^{17.5}\) to \(10^{18.8}\) cm. This empirically established fact is also interesting because the absence of polycentric systems on the S-axis coincides with the lower part - the "trough" - of the nuclear-galactic wave (CLASS #10) located between the two humps of the MEGAINTERVAL on the SW model (see Fig. 1.34). However, it is in this size range that many systems with strong signs of monocentricity are located, e.g.: QUASARS, GALACTIC NUCLEI, AND PLANETARY NEBULAE. GAS GALACTIC NEBULAE (CLASS #10). The most symmetric of these are known to be planetary nebulae, which most often resemble torus21 in shape (see Fig. 1.40A). In the closest of them, fibers are found running from the center to the periphery, like spokes in a wheel. Since these details are at the resolution limit of the telescope, astronomers assume22 they are present in all planetary nebulae, although they are not seen in distant ones. Most planetary nebulae are \(10^{17}\)-\(10^{18}\) cm in size and have a very symmetrical shape, despite having very low densities of about \(10^{-20}\) g/cm\(^3\).

Absolutely unsymmetrical and almost chaotic are diffuse nebulae like the Crab Nebula (see Fig. 1.40B), which are the remnants of supernovae explosions. Their typical sizes are \(10^{19}\)-\(10^{20}\) cm.

Comparing these two types of nebulae, which consist of the same type of rarefied gas, we can note the following. Those nebulae that have dimensions corresponding to the lowest point of the HW half-wave (this point according to our model has increased stability) have increased central symmetry (torus shape and radial symmetry of spokes).

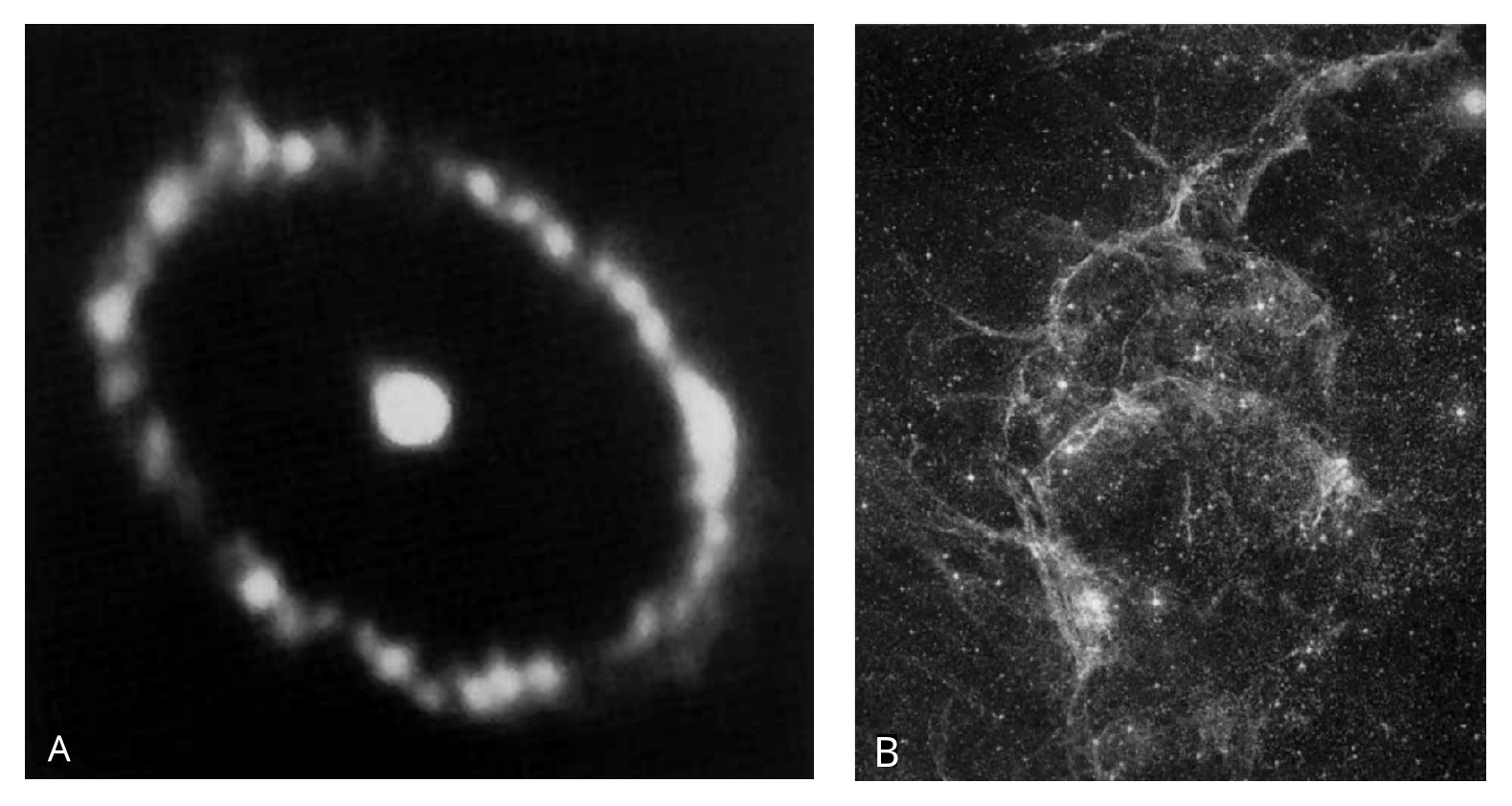Fig. 1.40. А. A planetary nebula whose dimensions are close to \(10^{17}\)-\(10^{18}\) cm. The ring symmetry is clearly visible. The radial symmetry of the "spokes" is not visible, although detectable. B. Crab Nebula, whose dimensions are close to \(10^{20}\) cm. Chaotic fibrous structure lacks any sign of symmetry

And the nebulae, whose sizes correspond to the unstable zone on the SW model, have an asymmetric shape. At first glance, the reason for the difference in symmetry is in the nature of the process of nebula formation, because torus planetary nebulae are formed by slow and quiet detachment of the shells of red giants (KG), and nebulae such as the Crab Nebula - as a result of a grandiose explosion of supernovae (SN), which leads to a rapid process of mixing of matter and loss of any symmetry. This explanation could be accepted if it were not for some recent observations. They have shown that the remnants of supernova explosions undergo a stage of higher shape symmetry at sizes close to \(10^{17}\)-\(10^{18}\) cm. In addition, within the chaotic fibers we can often observe23 quite symmetric structural details - bright rings with sizes around \(10^{16.7}\) cm. Consequently, the explosive dynamics of the process does not affect the possibility of the formation of symmetric shapes, and the main thing in this case is not the difference in the dynamics of the process, but the scale level: if it corresponds to the zone of increased stability and symmetry (i.e., the lower fossa of the half-wave of the HW), then even inside chaotic nebulae symmetric structural parts are formed.

NUCLEI OF GALAXIES (CLASS NO. 10). First, we present data on their sizes and some features. According to E. J. Vilkovisky24, galactic nuclei consist of an inner structure (the nucleus proper), whose dimensions lie in the range \(10^{17}\)-\(10^{18}\) cm, and an outer shell (\(3 \times 10^{18}\)-\(10^{20}\) cm). According to B. Balik and R. Brown25, the nucleus of our Galaxy is a very compact radio source with dimensions of the order of \(10^{16}\) cm.

"Spiral galaxies, both those observed in plan view and those facing us with their edges, usually have a well-defined nucleus. This is the brightest region of a spiral galaxy. The nucleus is also observed in SO lenticular galaxies. In elliptical galaxies, signs of it can be found only in the most compressed galaxies E6-E7. The nucleus is the densest region of the galaxy. It's natural. And in other stellar systems - globular clusters, scattered clusters - the central regions have the highest stellar density. However, studies in recent years have shown that the nuclei of galaxies... have a number of important features. Thus, it turned out that in the very center of the nucleus one can usually find another strong compaction - a nucleus... It rotates like a solid body."26

The core is about 10 parsecs in size, or \(3 \times 10^{19}\) cm, has a rotation period of about 500,000 years, and is 20,000 times denser than the neighborhood of the Sun.

"According to V. A. Ambartsumian, nuclei are the main active region in galaxies and the place of concentration of superdense matter. Galactic explosions of energy-saturated superdense matter eject its parts from the nucleus together with the accompanying stars and gas along the spiral lines, where, as a result of continuous crushing of superdense matter parts, the process of star formation and diffuse matter extraction continues."27

According to some estimates28, the compact nucleus at the center of our Galaxy is no larger than \(10^{18}\) cm.

The nuclei of galaxies often undergo violent and inhomogeneous processes29. This indicates some macro heterogeneity inside the nuclei, so it is difficult to bring their structure to a simple gravitational sphere. "Active galactic nuclei - which include quasars - have become a new class of astronomical objects. They are the most powerful and the most turbulent objects in the Universe."30

Faintly luminous nebulae have recently been discovered around some QUASARs. For their ephemeral appearance, British and American astronomers gave them the beautiful name "fuzz" - fluff. True, their size turned out to be the same as the size of galaxies. Thus, some quasars are located in the center of giant nebulae (harbingers of the appearance of galaxies there?), "like a dense, tiny poplar seed in its downy shell."31

According to B. A. Vorontsov-Vel'yaminov32, the sizes of quasars are \(10^{15}\)- \(10^{17}\) cm, and according to Vilkovisky33, they are \(10^{14}\)- \(10^{17}\) cm. According to other data34, the sizes of quasars can reach larger values: quasar 3C345 has a cross section of 6 \(\times\) \(10^{18}\) cm, and typical sizes of quasars lie in the range of 3 \(\times\) \(10^{18}\)-6 \(\times\) \(10^{19}\) cm. Such a discrepancy in the estimation of the average sizes of quasars is probably due, first of all, to the fact that they represent an inhomogeneous multilayer formation with a sparse shell, nuclear region and core, and therefore each of the experts chooses one or another formation as a boundary. Thus, in the center of the MEGAINTERVAL, in the lowest point of the potential stability trough, - between the two humps of SW, we find (see Fig. 1.35) MP-structures with a central significant core (and possibly even with a spherical shape). At the same time, all these MF-structures occupy on the S-axis exactly the range that is free of pure polycentric systems. Even if in the future it will be possible to detect polycentric clusters of stars with sizes from \(10^{17.5}\) to \(10^{18.8}\) cm, these will be very rare structures, since they have not been detected in many past observations.

Vorontsov-Vel'yaminov in 1969 expressed35 a hypothesis according to which KVASARs, which are splitting into parts (like a dividing cell), consist of components, each of which has its own speed of removal from the observer from the Earth. This explains a number of anomalies in their spectrum, which are quite impossible to explain from the standpoint of the uniform spherical model.

By the way, astrophysicists believe that fragments of a divisioning quasar subsequently turn into galactic groups. Does this not remind us of the process that goes exactly 20 orders of magnitude to the left on the S-axis, namely, the process of cell division, which can result in a colony of cells or develop a multicellular organism.

Since quasars are located on the same place of the Mega-interval as the cell on the Macro-interval (see Fig. 1.34 and Fig. 1.26), their division into parts from the point of view of scale similarity is quite probable. In this case, they can be in a mononuclear stable position of growth and substance accumulation or in a polynuclear (in the simplest case - binary) phase of active division with an obviously heterogeneous structure. Evidence in this favor is the fact that 60% of all radio sources (nuclear regions of galaxies) are double.

The double structure is also observed in some quasars36.

Unfortunately, direct observation of galaxy nuclei is impossible, because they are usually covered by a shell hundreds of times larger than their size. The sources of information are some indirect observations: gas velocity, rotation periodicity, radiation uniformity, etc. This allows us to build models of galaxy nuclei, which probably have some signs of monocentricity: spherical shape, nucleus, but they are unlikely to have shells, and they probably do not resemble giant stars in their internal structure. It is tempting to give their structure a semblance of similarity to a living cell, but this PROPOSAL requires very careful testing. According to astrophysics37, the main source of energy for the active nuclei of galaxies is black holes (BHs). If this is true, then the sizes of galactic PDs are calculated using the formula:

\[R_g = \frac{2GM}{c^2} = 3 \times 10^5 \cdot \frac{M}{M_\odot} \text{ cm}. \tag{1.8}\]

The average masses of galaxies, depending on their type, range from \(10^9\) to \(10^{11.5}\) solar masses38.

...Determinations of galaxy masses often refer only to their nuclear regions" (B. A. Vorontsov-Vel'yaminov, op. cit. p. 163). Therefore, to get a theoretical possibility to compare the size ranges of the existence of galactic BHs, let us make the following PROPOSAL. Let us assume that the mass of a BH is commensurate with the mass of the entire galaxy.

According to more precise estimates, the range is wider: from \(10^6\) to \(10^{13}\) solar masses. Consequently, the possible PD sizes for galaxies calculated by formula (1.8) lie in the range from \(10^{11}\) cm to \(10^{18}\) cm. However, given that small galaxies have practically no nuclei, much less active ones, the range of PDs for galaxies should be reduced by a minimum threshold, and most likely it starts at \(10^{16}\) cm. Therefore, with a certain degree of probability we can BELIEVE that the active nuclei of galaxies in the form of black holes have sizes from \(10^{16}\) to \(10^{18}\) cm. These are the regions of space from which energy is expelled. And note that it is this range of sizes that corresponds to the lower zone of the nuclear galactic half-wave in the SW. Recall that it is in such lower zones of the HW that the main energetic processes take place (atomic nuclei are 30 orders of magnitude to the left, stellar nuclei are 10 orders of magnitude to the left). This once again testifies to the naturalness of the classification properties of our model SW (see Fig. 1.7).

GALAXIES (CLASS NO. 11). Next to globular clusters on the S-axis are dwarf galaxies, followed by ordinary galaxies.

Most galaxies are typical polycentric structures consisting of many stars, just as atoms and molecules make up bodies in the Macro-interval. Only some types of galaxies have a well-defined and active nucleus. These are mostly spiral galaxies (see Fig. 1.41), which occupy the top of the second ridge of the Mega Interval.

By the way, all kinds of galaxies cannot transform into each other because they have different masses and different angular momentum of rotation39. Both, according to modern physics, are neither lost nor gained. That is, large galaxies have never been small, and vice versa.

If this is indeed true, then small galaxies (\(10^{20}\)-\(10^{22}\) cm), which are mostly elliptical, have an internal structure that is mostly polycentric (no shells or nuclei). The outer shape tends to be spherical (ellipsoid).

Pebbles on the shore are analogous to small elliptical galaxies (EGs). The ratio of the size of a pebble to an atom inside it is almost the same as the ratio of the size of an elliptical galaxy to a star. The shape of pebbles and EGs is ellipsoidal. There are usually no nuclei. The size of the pebbles is such (~10 cm) that they occupy the left slope of the SW ridge, the top of which has a coordinate of \(10^2\) cm. The dimensions of the EGs are such that they occupy the left slope of the SW ridge with its apex at \(10^{22}\) cm. The distance between them is 20 orders of magnitude along the S-axis.

Fig. 1.41. Spiral galaxy with a pronounced nuclear region and a satellite

Large galaxies (\(10^{22}\)-\(10^{23}\) cm), which are mostly spiral galaxies, have a shape far from a sphere, but almost always have a nucleus.

Thus, we see that MP structures are mostly common in the world of galaxies.

The most numerous are elliptical galaxies and dwarf galaxies (of the Sculptor type)40. Astronomers came to this conclusion after calculating the ratio of the number of elliptical and spiral galaxies. Yu. I. Efremov, having processed the data of galaxy catalogs, came to the conclusion that "elliptical galaxies are about 100 times more numerous than spiral galaxies."41

Since most elliptical galaxies are dwarfs and spiral galaxies are giants, the following becomes clear.

The bulk of galaxies, which have small sizes (up to \(10^{21-22}\) cm), are closer to the polycentricity pole; large galaxies, which are mostly spiral, have a MP structure with an obligatory nucleus.

According to T. A. Aghekyan42, in addition to spiral galaxies, SO lenticular galaxies and some of the most compressed elliptical galaxies, such as E6-E7, have nuclei.

Giant spiral galaxies on the S-axis are followed by nests of galaxies, pair galaxies, and other systems composed of galaxies. This TRANSITION FROM WHOLE OBJECTS TO THEIR SYSTEMS begins exactly 10 orders of magnitude after the analogous transition from stars to their pairs and clusters, 20 orders of magnitude after the transition of biosystems from organisms to their groups, and exactly 40 orders of magnitude after the transition from atoms to molecules (see Fig. 1.7). Virtually all galaxy clusters, their superclusters, and giant cells from them are all polycentric systems. They have no distinguished core, shells, or spherical shape.

The METAGALACTIC STRUCTURE is also POLYCENTRIC (see Fig. 1.42) up to the size of \(10^{27}\) cm. In any case, astronomers have not been able to find a nucleus in the Metagalaxy.

So, in the world of galaxies (CLASS #11), polycentrism mainly dominates, since it is very rare to find galaxies with at least two clear signs of monocentrism (nucleus and spherical shape). The author failed to find at least one example of an M-structure in the galactic world, so we can confidently assert that monocentrism in its pure form, which is characteristic of the left ridge of the MEGAINTERVAL, is absent on its right ridge.

Fig. 1.42. Structure of the Metagalaxy. This map shows the distribution of two million galaxies (ten billion galaxies in all) for a section of the sky. The galaxies are clustered in super clusters that form layers and ribbons separated by large voids; this resembles foam in structure

Let us summarize the analysis of the MEGAINTERVAL by considering the scheme (see Fig. 1.35).

The first order of the Megainterval (small planets, asteroids) is occupied by transitional forms; here, as we move to the right, polycentrism gradually gives way to monocentrism. This is manifested first of all in the appearance of spherical form.

It can be PROPOSED that polycentrism, caused by the corresponding distribution of atoms in the crystalline structure of large bodies, is replaced by megacluster polycentrism at this section of the S-axis (mascons, separations of crustal blocks, and the inhomogeneous structure of pulsars). If this is true, then megacluster polycentrism manifests itself in bodies whose sizes correspond to the first and second orders of the Megainterval.

Already from the middle of the first order, the chaotic form is replaced by a monocentric - spherical form (example - Mimas). If we focus only on the form, then from the middle of the first order up to the fifth order monocentrism dominates the S-axis indiscriminately.

The core-shell features of monocentrism apparently begin to appear from the middle of the second order (e.g., the nucleus of the Moon or Mercury). It is from this point of the S-axis and up to the sixth order (the top of the first ridge) that monocentrism dominates in all three of its manifestations.

After the first crest, monocentric structures occur for another two to two and a half orders, albeit very rarely: we are talking about the largest stars, which both in mass and number occupy a very inconspicuous fraction of the total stellar class. However, from the crest of the first wave, i.e., starting from the sixth order of the MEGAINTERVAL, polycentrism appears, which then dominates all the remaining 15 orders.

The only place on the MEGAINTERVAL where we see an obvious return of monocentrism is in its middle, the POTENTIAL trough OF stability, which occupies the eleventh order, plus or minus another order (planetary nebulae, galactic nuclei, quasars).

The entire rise of the second ridge is populated mainly by polycentric structures in which the elements of the systems are stars (star clusters, dwarf galaxies). On the left slope of the second ridge, one can detect some return of monocentrism. From its top, polycentric structures of the second kind, consisting of galaxies rather than stars, begin to appear. The descent from the second SW ridge for galaxies is polycentric completely up to the end of the Megainterval (galaxy clusters of all kinds).

On the twentieth order, we see the same undivided dominance of polycentrism as on the twentieth order of MICRO-INTERVAL and MACRO-INTERVAL (the fibrous, chaotic structure of the Metagalaxy).

Star globular clusters and spherical galaxy clusters deviate from the described sequence. Both of them are located in the zone of intersection of the S-axis with the SWS.

  1. Zharkov V. N. Internal Structure of the Earth and Planets. Moscow: Nauka, 1978. P. 181. ↩

  2. Xanfomaliti L. V. Planets Rediscovered. Moscow: Nauka, 1978. P. 20. ↩

  3. Struve O., Linds B., Pillans E. Elementary Astronomy. Moscow: Nauka, 1967. P. 52. ↩

  4. Allen K. W. Astrophysical Magnitudes. M.: Mir, 1977. P. 215. ↩

  5. Zharkov V. N. Internal Structure of the Earth and Planets. M.: Nauka, 1978. P. 183. ↩

  6. Xanfomaliti L. V. Planets Rediscovered. Moscow: Nauka, 1978. P. 16. ↩

  7. Alven H., Arrhenius G. Evolution of the Solar System. M.: Mir, 1979. ↩

  8. Alven H., Arrhenius G. Evolution of the Solar System. M.: Mir, 1979. P. 368. ↩

  9. Shklovsky I. S. Stars. Their birth, life and death. Moscow: Nauka, 1977. P. 327. ↩

  10. Shklovsky I. S. Stars. Their birth, life and death. Moscow: Nauka, 1977. P. 298. ↩

  11. Shklovsky I. S. Stars. Their birth, life and death. Moscow: Nauka, 1977. P. 325-326. ↩

  12. Vorontsov-Vel'yaminov B.A. Essays on the Universe. Moscow: Nauka, 1969. P. 566-567. ↩

  13. Allen K. W. Astrophysical Magnitudes. M.: Mir, 1977. P. 369. ↩

  14. Vilkovisky E. Y. Quasars. M.: Nauka, 1985. P. 122. ↩

  15. Vilkovisky E. Y. Quasars. M.: Nauka, 1985. P. 146-147. ↩

  16. Aghekyan T. A. Stars, Galaxies, Metagalaxy. M.: Nauka, 1981. P. 179. ↩

  17. Aghekyan T. A. Stars, Galaxies, Metagalaxy. M.: Nauka, 1981. P. 186. ↩

  18. Lindgenfelter R. E., Ramati R. On the nature of radiation due to annihilation of electrons and positrons from the region of the galactic center // Galactic Center. M.: Mir, 1984. P. 177. ↩

  19. Aghekyan T. A. Stars, Galaxies, Metagalaxy. M.: Nauka, 1981. P. 181. ↩

  20. Suchkov A. A. Galaxies familiar and mysterious. Moscow: Nauka, 1988. P. 120. ↩

  21. Suchkov A. A. Galaxies familiar and mysterious. Moscow: Nauka, 1988. P. 135. ↩

  22. Vorontsov-Vel'yaminov B. A. Extragalactic Astronomy. M.: Nauka, 1978. P. 428. ↩

  23. Vilkovisky E. Y. Quasars. M.: Nauka, 1985. P. 64, 98. ↩

  24. Martynov D. Ya. Course of General Astrophysics. M.: Nauka, 1979. P. 452. ↩

  25. Vorontsov-Vel'yaminov B. A. Extragalactic Astronomy. M.: Nauka, 1978. P. 462. ↩

  26. Vorontsov-Vel'yaminov B. A. Extragalactic Astronomy. M.: Nauka, 1978. P. 417. ↩

  27. Suchkov A. A. Galaxies familiar and mysterious. Moscow: Nauka, 1988. P. 151. ↩

  28. Vorontsov-Vel'yaminov B. A. Extragalactic Astronomy. M.: Nauka, 1978. P. 113. ↩

  29. Shklovsky I. S. Stars. Their birth, life and death. Moscow: Nauka, 1977. P. 213-214. ↩

  30. Allen K. W. Astrophysical quantities. Zh-M.: Mir, 1977. P. 295. ↩

  31. Mukhin K. N. Physics of atomic nucleus // Experimental nuclear physics. Т. 1. M.: Atomizdat, 1974. P. 50. ↩

  32. Chechev V. R., Kramarovsky Ya. M. Radioactivity and the Evolution of the Universe. Moscow: Nauka, 1978. ↩

  33. Chechev V. R., Kramarovsky Ya. M. Radioactivity and the Evolution of the Universe. Moscow: Nauka, 1978. P. 40. ↩

  34. Chechev V. R., Kramarovsky Ya. M. Radioactivity and the Evolution of the Universe. Moscow: Nauka, 1978. P. 44. ↩

  35. Islam J. N. Sky and Telesc. 1979, 57, I, P. 13-18. ↩

  36. Animal life. Т. 1. M.: Prosveshchenie, 1968. P. 71. ↩

  37. Animal life. Т. 1. M.: Prosveshchenie, 1968. P. 139. ↩

  38. Green N., Stout W., Taylor D. Biology. T. 1. M.: Mir, 1996. P. 22. ↩

  39. The life of animals. T. 1. M.: Enlightenment, 1968. P. 159. ↩

  40. The life of animals. T. 1. M.: Enlightenment, 1968. P. 120-125. ↩

  41. The life of animals. T. 1. M.: Enlightenment, 1968. P. 98. ↩

  42. Afanasyev Yu. I., Korolev V. V., Kotovsky E. F. Cell nucleus and some questions of cytogenetics. Moscow: Nauka, 1971. P. 19. ↩