S-dynamics of the Universe
So far we have considered a static picture of the scale symmetry of the Universe, deliberately avoiding, as far as possible, examples of dynamic symmetry. This technique was necessary for us in order for the reader to form some image of the CARCASE OF THE MASSIVE SPACE OF THE UNIVERSE so that the mentioning of any dimensions automatically evokes associations with the world of specific universal systems and their scale classes.
However, the mosaic composed of pieces of empirical facts has its own dynamic life and obeys the laws of symmetry of motion along the S-axis. Therefore, we will pass from STATICS to DYNAMICS of the large-scale structure of the Universe. And here no less, if not more, mysterious and surprising regularities are waiting for us.
Preceding the conclusions of this part, we note that the dynamics of object motion along the S-axis can best be described based on the image of the hilly "surface" of the Stability Wave. We will show that there are often processes in which objects seem to strive to roll down its slopes to the lowest points. Recall that this process is accompanied by a very significant increase (or decrease) in the size of these objects.
To make it easier for the reader to navigate in the sea of new facts, we recommend keeping before you (mentally or actually) a picture of the SW (see Fig. 1.7) and imagine yourself sliding on a sled (or skis) of large-scale movement, when the movement up the slopes of the SW requires energy expenditure, and the movement down occurs "with a breeze", i.e. the energy is released. At the same time, both on the slope and especially at the top, you can get a foothold and look around. So, let's go on our amazing walk along the slopes of SW.
Let us start with a few vivid and figurative examples on the STAR MASTER DIAPASON (see Fig. 2.1).
All stars sooner or later end their active life. The process is different for stars of different masses. PLANETARY NEBULAE. According to modern astrophysical ideas 1, planetary nebulae form at the final stage of development of red giants, when they shed their outer shell. It turns into a planetary nebula, and the remaining core gradually turns into a white dwarf, the minimum size of white dwarfs is \(10^{8}\) cm. The radius of detachment of the shell is about \(10^{13}\) cm, and its maximum size after expansion reaches \(10^{18}\) cm.
Planetary nebulae in the Galaxy are quite numerous, they are even considered the main suppliers of cosmic dust. So the process of their formation from red giants has been repeated many times in the Universe and is statistically significant. Now let us pay attention to the fact that on the S-axis this process goes symmetrically in both directions: in the direction of size increase - from 13th order to 18th order there is a shift by 5 (!) orders of magnitude; and in the direction of decrease - from 13th order to 8th order there is a decrease by 5 orders of magnitude (see Fig. 2.1). The distance between the two "shards" of the red giant on the S-axis reaches 10 orders of magnitude.
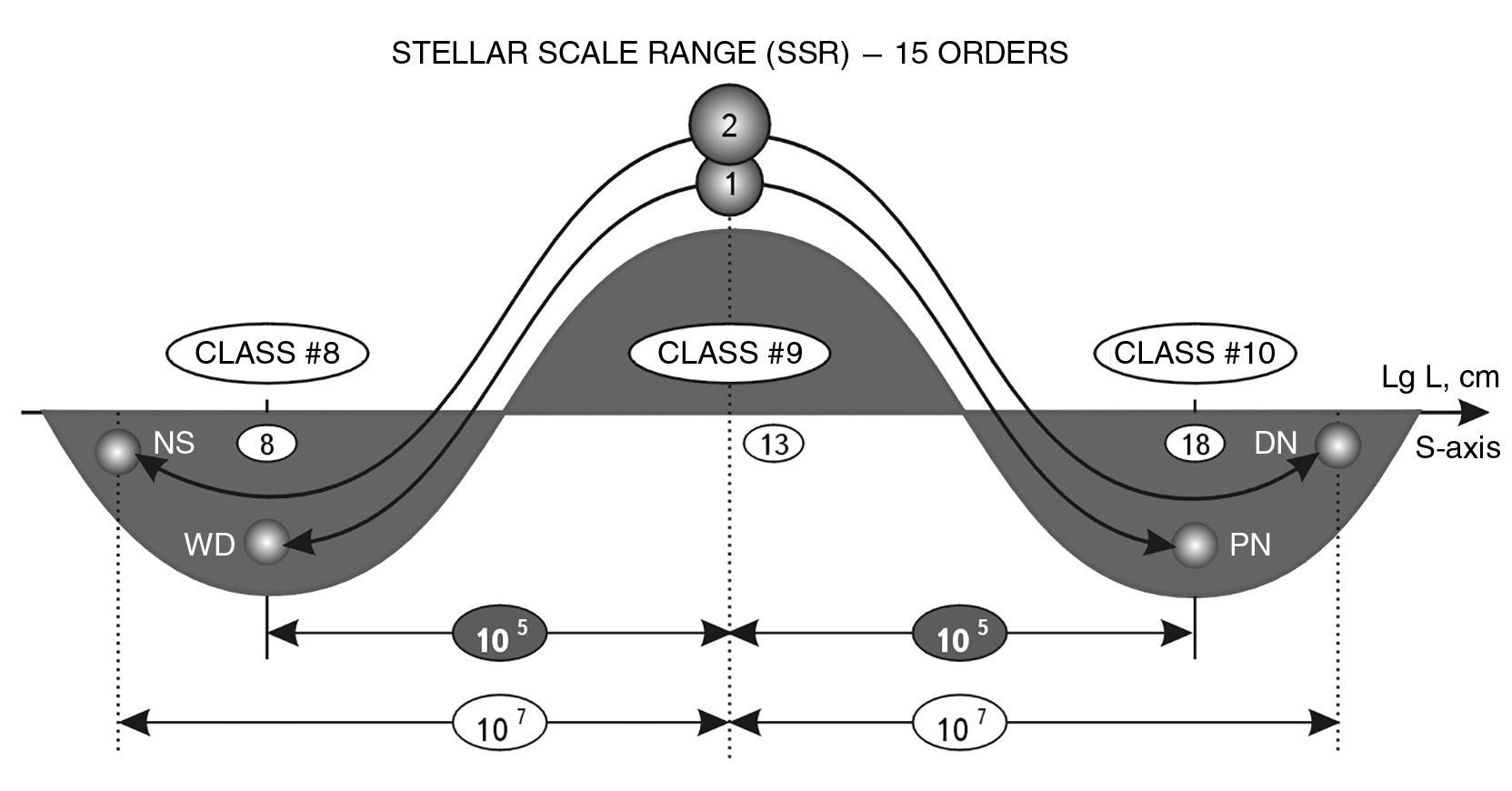 Fig. 2.1. Symmetry of stellar death dynamics on the S-axis. Star 1 (M<M0) explodes along the S-axis into two "fragments": PT - planetary nebula and BK - white dwarf, which are at a distance of 5 orders of magnitude from the initial point of collapse. Star 2 (M>M0) splits along the S-axis into two other "fragments": DT - diffuse nebula and NS - neutron star. (M is the mass of the star, M0 is the mass of the Sun)
Fig. 2.1. Symmetry of stellar death dynamics on the S-axis. Star 1 (M<M0) explodes along the S-axis into two "fragments": PT - planetary nebula and BK - white dwarf, which are at a distance of 5 orders of magnitude from the initial point of collapse. Star 2 (M>M0) splits along the S-axis into two other "fragments": DT - diffuse nebula and NS - neutron star. (M is the mass of the star, M0 is the mass of the Sun)
DIFFUSE NEBULAE. Such nebulae, according to theoretical considerations, can be formed only after the explosion of a star with a mass exceeding 2-10 solar masses 2. According to reference data 3 , stars with such masses are either supergiants of all spectral classes with sizes \(10^{12.45}\)- \(10^{14}\) cm, or main-sequence giants with sizes greater than \(10^{12.4}\) cm.
For a short time on cosmic scales, the shell, thrown off by the exploded star at a speed of 10,000 km/s, expands maximally to a size of about \(10^{20}\) cm and turns into "faint fibers and fragments" - a diffuse nebula. At the same time, the supernova core shrinks to the size of a neutron star, with a minimum diameter of \(10^{6}\) cm.
If we assume that, on average, the diameter of an exploding star is \(10^{13}\) cm, then on the S-axis we again observe a symmetric dispersion of "fragments": the shell of the star moves 7 orders of magnitude to the right, and the core moves the same amount to the left (see Fig. 2.1). So the question arises. Why do all stars, ending their life, "divide" into two parts, each of which moves along the S-axis symmetrically in opposite directions? Let us note for now only the obvious.
We have an example of DYNAMIC MASTER SYMMETRY, to which the most widespread form of matter in the Universe - stellar matter, which makes up 99% of its mass, is subordinated. At first glance, it is impossible to find a physical explanation for this regularity. After all, when we consider the symmetrical dispersion of grenade fragments from the center of the explosion, we understand that the symmetrical expansion force of the blast wave acts on them. When we consider the collision of two identical billiard balls on the table, rolling at the same angles in symmetrical directions, we realize that the law of mechanics - the law of conservation of momentum - is acting here.
What forces can act along the S-axis to bring to symmetry such different processes as the expansion of the shell of a star and the compression of its core? After all, we are talking about symmetry in the dynamics of processes that in one case go inward to the object, and in the other case - outward to it. Maybe in nature, the momentum is preserved in the scale dimension as well?